В прямоугольном треуголнике DCE с прямым углом C проведена биссектриса EF причём FC=13см найдите расстояние от точки F до прямой DE
Ответы на вопрос
Ответил badakur
0
Так как расстояние всегда связано с перпендикулярностью, проведем отрезок FH перпендикулярно прямой DE. Точка H принадлежит гипотенузе DE.
Треугольники ECF и EHF равны по общей гипотенузе FE и равными острыми углами CEF и HEF (по условию EF - биссектриса).
Следовательно, FC = FH (соответственные катеты).
FH - 13 см.
Ответ: расстояние от точки F до прямой DE равно 13 см.
Треугольники ECF и EHF равны по общей гипотенузе FE и равными острыми углами CEF и HEF (по условию EF - биссектриса).
Следовательно, FC = FH (соответственные катеты).
FH - 13 см.
Ответ: расстояние от точки F до прямой DE равно 13 см.
Ответил Даниил221928
0
спасибки тебее
Ответил Banabanana
0
Кратчайшее расстояние от точки до прямой - перпендикуляр.
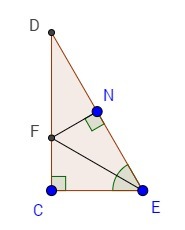
Построим перпендикуляр FN.
Рассмотрим ΔFCE и ΔFNE:
∠СЕF = ∠NЕF = 90°
EF - общая гипотенуза
∠FЕС = ∠FEN (т.к. EF биссектриса ∠СЕD)
Следовательно, ΔFCE = ΔFNE.
В равных Δ против равных углов лежат равные стороны ⇒ FN=FC=13 cм
Ответ: 13 см.
Построим перпендикуляр FN.
Рассмотрим ΔFCE и ΔFNE:
∠СЕF = ∠NЕF = 90°
EF - общая гипотенуза
∠FЕС = ∠FEN (т.к. EF биссектриса ∠СЕD)
Следовательно, ΔFCE = ΔFNE.
В равных Δ против равных углов лежат равные стороны ⇒ FN=FC=13 cм
Ответ: 13 см.
Приложения:
Новые вопросы
Физика,
2 года назад
Химия,
2 года назад
Литература,
8 лет назад
География,
9 лет назад
История,
9 лет назад