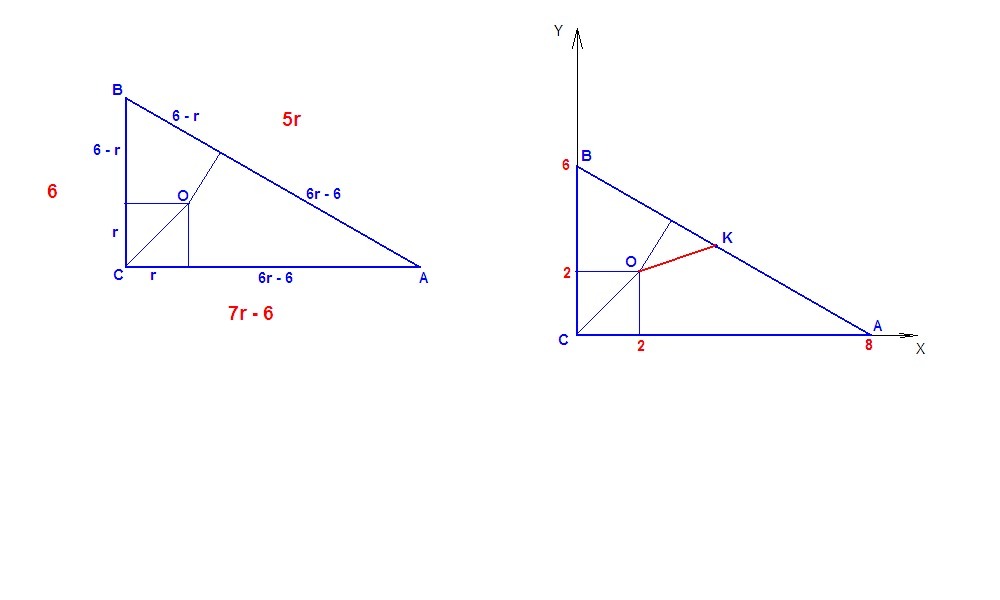
в прямоугольном треугольнике авс гипотенуза ав в 5 раз длиннее радиуса вписанной окружности, меньший катет bc равен 6 Найти расстояние между центром вписанной и описанной окружностью
Ответы на вопрос
Пусть О - центр вписанной окружности.
r - радиус вписанной окружности.
Отрезки касательных, проведенных из одной точки, равны, поэтому
CD = CE = r
BD = BF = 6 - r
Так как гипотенуза в 5 раз больше радиуса вписанной окружности, то
АВ = 5r
AF = AB - BF = 5r - (6 - r) = 6r - 6
AE = AF = 6r - 6
Учитывая, что АВ = 5r, BC = 6 и AC = r + 6r - 6 = 7r - 6, по теореме Пифагора составим уравнение:
АВ² = BC² + AC²
25r² = 36 + (7r - 6)²
25r² = 36 + 49r² - 84r + 36
24r² - 84r + 72 = 0
2r² - 7r + 6 = 0
D = 49 - 48 = 1
r = (7 + 1)/4 = 2 или r = (7 - 1)/4 = 3/2
AC = 7 · 2 - 6 = 8 AC = 7 · 3/2 - 6 = 10,5 - 6 = 4,5
Так как ВС меньший катет по условию, то
r = 2, AC = 8, AB = 10.
Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
Пусть К - середина гипотенузы. Тогда ОК - искомый отрезок.
Поместим треугольник в прямоугольную систему координат (как на рисунке).
Тогда центр вписанной окружности имеет координаты:
О(2 ; 2),
а центр описанной окружности:
К((8 + 0)/2 ; (6 + 0)/2 ) (координаты середины отрезка равны полусумме координат его концов)
К(4 ; 3)
Найдем длину отрезка через координаты его концов:
ОК² = (2 - 4)² + (2 - 3)² = 4 + 1 = 5
ОК = √5