В прямоугольном треугольнике ABC ( угол С равен 90°) АВ=20см угол АВС=30°
С центром в точке А проведено окружность Каким должен быть радиус чтобы:
1) окружность касалась прямой BC
2) окружность не имела общих точек с прямой BC
3) окружность имеют две общие точки прямой BC

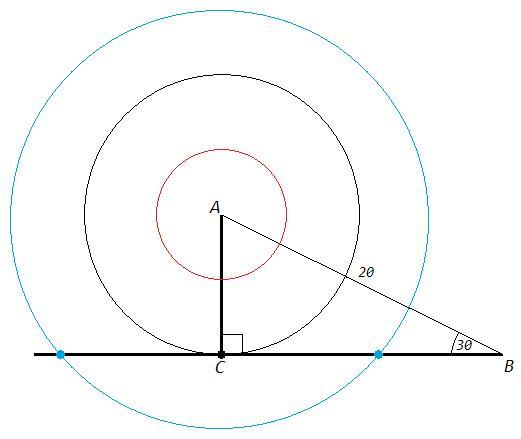
Расстояние от точки до прямой измеряется длиной перпендикуляра. AC⊥BC, AC - расстояние от точки A до прямой BC.

Катет AC лежит против угла 30 и равен половине гипотенузы AB. AC=AB/2=10.

1) если окружность касается прямой, то радиус равен расстоянию от центра окружности до прямой, R=10.

2) если окружность не имеет общих точек с прямой, то радиус меньше расстояния от центра окружности до прямой, R<10.

3) если окружность имеет две общих точки с прямой, то радиус больше расстояния от центра окружности до прямой, R>10.