В прямоугольном треугольнике ABC с прямым углом С, высота CD=24 см и отсекает от гипотенузы AB отрезок BD=18 см. Найдите AC
Ответы на вопрос
Ответил Аноним
0
...............................................
Приложения:
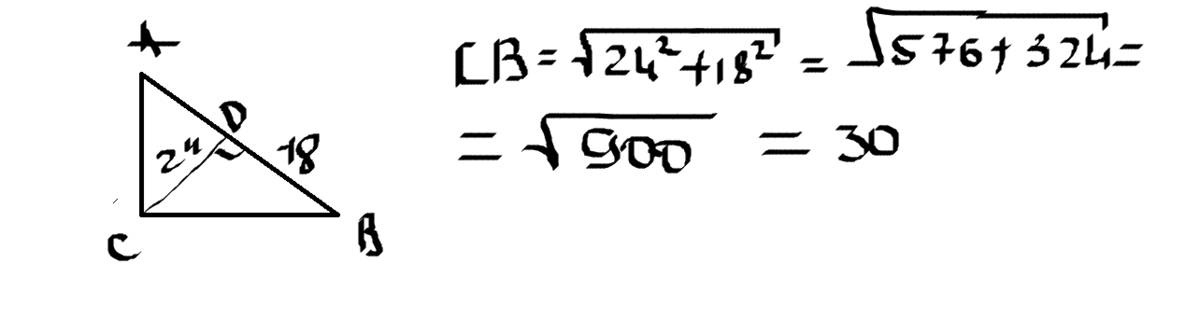
Ответил vipsuzdaltseva
0
В задаче нужно было найти AC, а не CB
Ответил Аноним
0
изменил пользователь вопрос
Ответил vipsuzdaltseva
0
Решение:
Рассмотрим (прямоугольный) треугольник абс. СД-высота, проведённая из вершины прямого угла, делит гипотенузу на отрезки, произведения который равны квадрату этой высоты. 24 в квадрате=576
Пусть x-это АД. 576=x умножить на 18. 18x=576.x=32-это АД.
Рассмотрим треугольник ADC. СD= 24, AD= 32. По теореме Пифагора(квадрат гипотенузы равен сумме квадратов катетов) запишем уравнение.
x в квадрате= 24 в квадрате + 32 в квадрате. x в квадрате= 576+1024. x в квадрате= 1600. x= 40-это AC.(см)
Ответ: AC= 40 см.
Рассмотрим (прямоугольный) треугольник абс. СД-высота, проведённая из вершины прямого угла, делит гипотенузу на отрезки, произведения который равны квадрату этой высоты. 24 в квадрате=576
Пусть x-это АД. 576=x умножить на 18. 18x=576.x=32-это АД.
Рассмотрим треугольник ADC. СD= 24, AD= 32. По теореме Пифагора(квадрат гипотенузы равен сумме квадратов катетов) запишем уравнение.
x в квадрате= 24 в квадрате + 32 в квадрате. x в квадрате= 576+1024. x в квадрате= 1600. x= 40-это AC.(см)
Ответ: AC= 40 см.
Приложения:
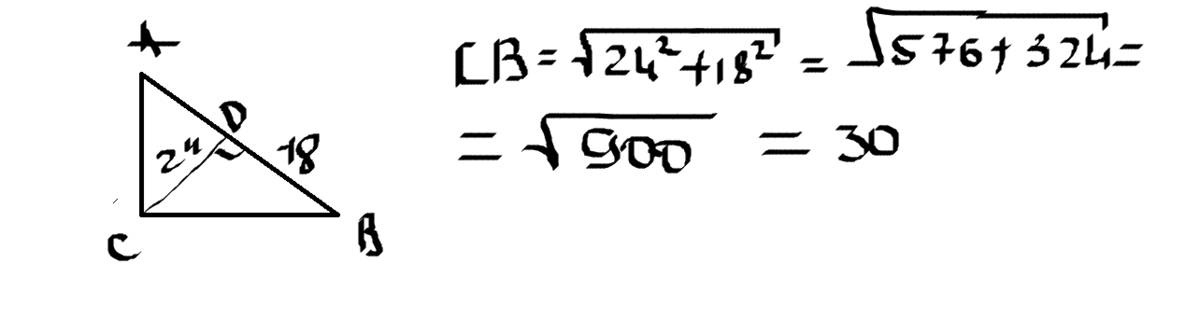
Новые вопросы
Русский язык,
2 года назад
Литература,
2 года назад
Математика,
9 лет назад
Математика,
9 лет назад
Математика,
9 лет назад