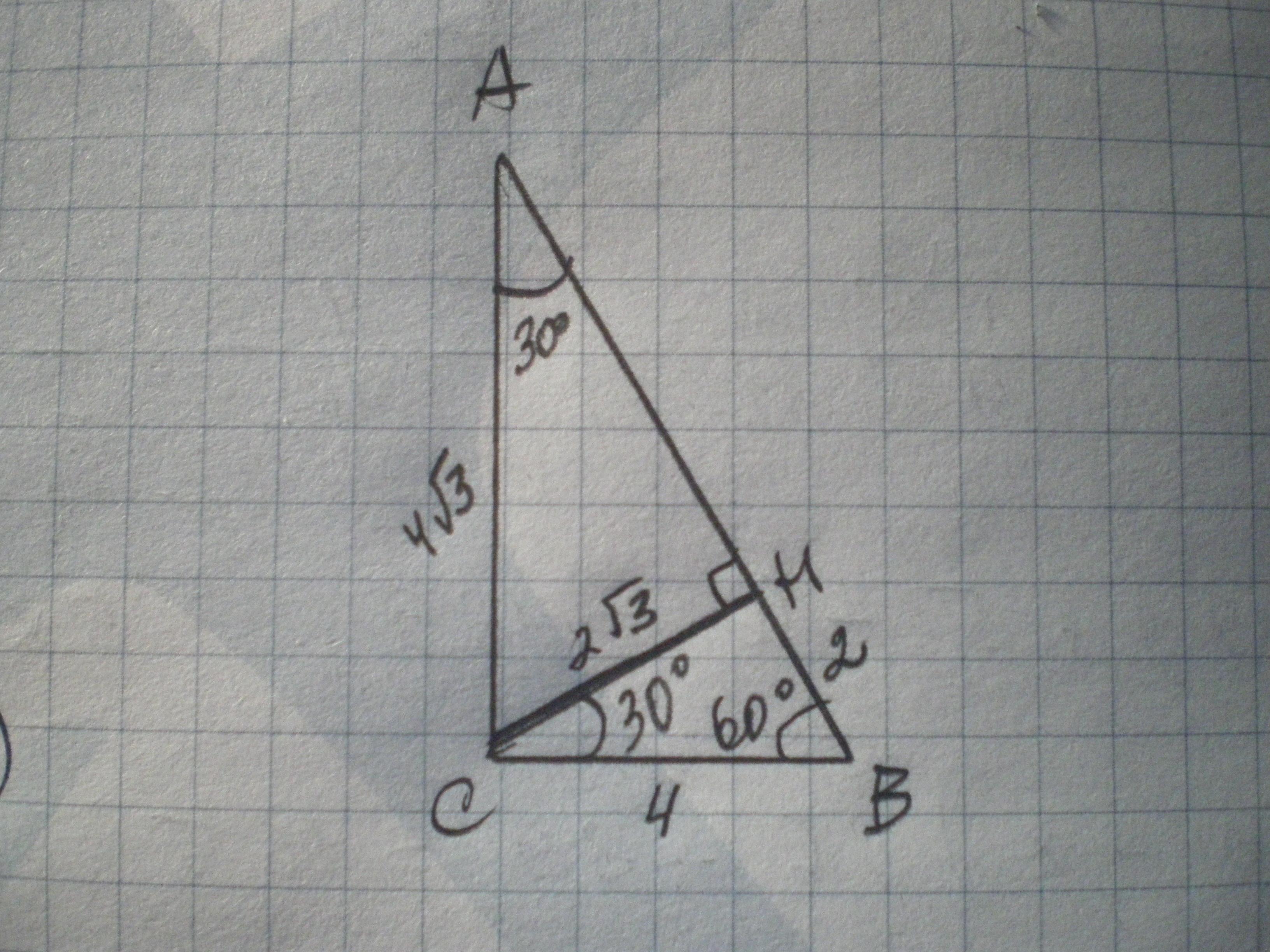
В прямоугольном треугольнике ABC с гипотенузой AB проведена высота CH. найдите HA, если угол B=60,BH=2 см
Ответы на вопрос
Ответил Пеппер
0
Дано: Δ АВС - прямоугольный, АВ - гипотенуза, СН - высота, ∠В=60°, ВН=2 см. Найти АН.
Решение:
рассмотрим Δ ВСН - прямоугольный, ∠ВСН=90-60=30°, тогда ВС=2ВН=4 см как катет, лежащий против угла 30°.
По теореме Пифагора
СН=√(ВС²-ВН²)=√(16-4)=√12=2√3 см.
Рассмотрим Δ АСН - прямоугольный, ∠А=90°-∠В=90°-60°=30°, тогда АС=2СН=4√3 см.
По теореме Пифагора АН=√(АС²-СН²)=√(48-12)=√36=6 см.
или: СН²=АН*ВН; 12=2*АН; АН=6 см.
Ответ: 6 см.
Приложения:
Новые вопросы