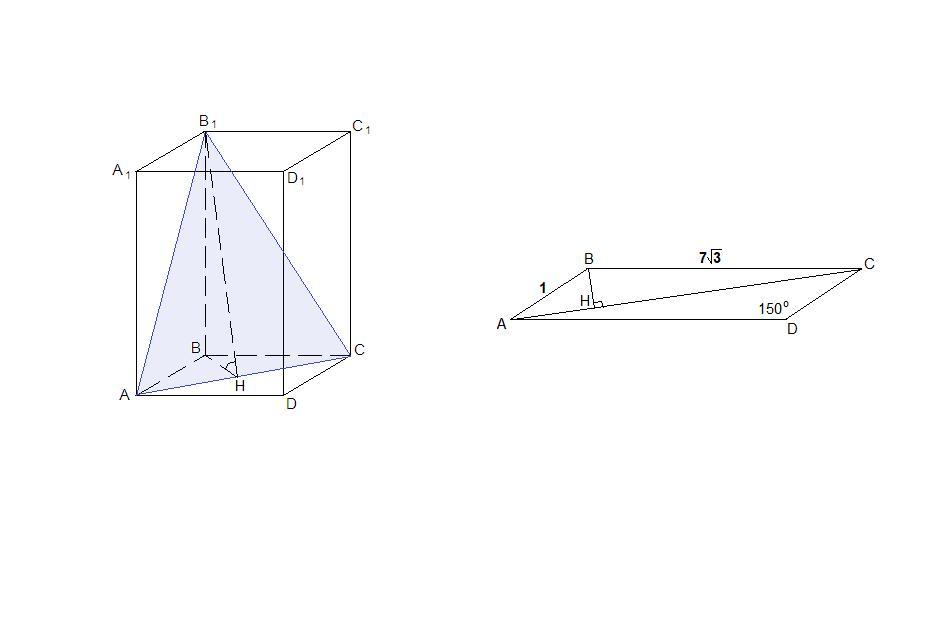
В прямом параллелепипеде ABCDA1B1C1D1 AB=1,BC=7(КОРЕНЬ)3,угол ABC=150. Через диагональ АС и вершину В1 проведена плоскость,составляющая с плоскостью основания угол 60. Найдите площадь боковой поверхности параллелепипида.

Ответ:

Объяснение:

Площадь боковой поверхности прямого параллелепипеда:

S = Росн · ВВ₁

Росн = 2(AB + BC) = 2(1 + 7√3)

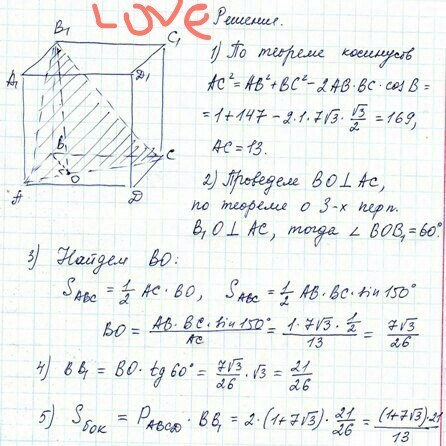
Проведем ВН⊥АС. ВН - проекция В₁Н на плоскость основания, значит

В₁Н⊥АС по теореме о трех перпендикулярах, ⇒

∠В₁НВ = 60° - линейный угол двугранного угла между плоскостями (В₁АС) и основанием.

ΔАВС: по теореме косинусов:

АС² = AB² + BC² - 2·AB·BC·cos∠B

AC² = 1 + 147 + 2 · 7√3 · √3/2 = 148 + 21 = 169

AC = 13

Sabc = 1/2 AB · BC · sin∠B = 1/2 · 7√3 · 1/2 =

Sabc = 1/2 AC · BH

ΔBB₁H:

tg∠B₁HB = BB₁ / BH

BB₁ = BH · tg60°