В правильной треугольной пирамиде SABC с вершиной Р и объемом 48 проведена плоскость, которая параллельна медиане основания BN и пересекает ребро SA в точке К, а боковое ребро SB в точке L, причем SK=1/2 SA, SL=1/3 SB. Найдите объем части пирамиды, лежащей ниже этой плоскости
Ответы на вопрос
Ответил Andr1806
0
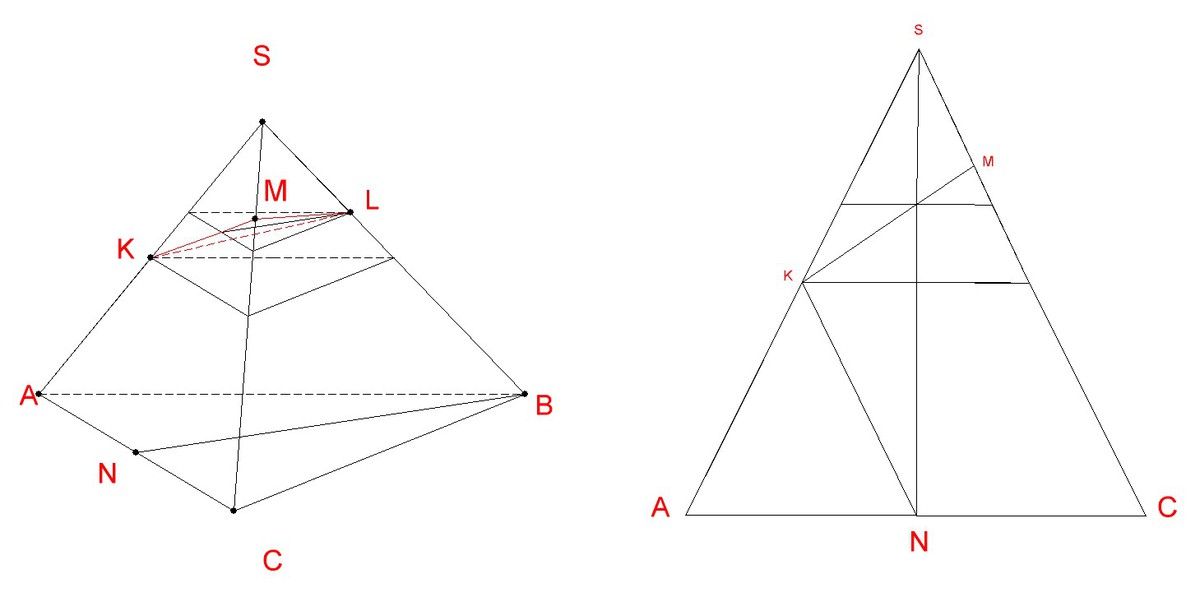
Первое. Прямые BN и KL - скрещивающиеся (по определению: две прямые в пространстве, не имеющие общих точек, и не являющиеся параллельными называются скрещивающимися). Надо провести плоскость через прямую KL, параллельную
прямой BN. Для этого надо через точку L провести прямую LM, параллельную BN. Тогда прямые KL и LM определяют нужную нам плоскость сечения. Проведем прямую SN (апофему грани ASC). Прямая LM пересекает SN в точке M, так как LM и BN лежат в одной плоскости NSB. Продолжим КМ до пересечения с SC в точке Q. Плоскость KLQ - плоскость искомого сечения.
Теперь надо найти объем пирамиды SКLQ, вычесть его из объема пирамиды SABC (48) и получим ответ.
Известно, что объемы тетраэдров, имеющих равные трехгранные углы, относятся как произведения длин ребер, образующих эти углы. Наша пирамида правильная, значит трехгранные углы при вершине S равны.
Докажем правильность данного выше утверждения для нашего случая.
Проведем высоты LH и BH1 в пирамидах LKSQ и ВASC. LH и BH1 параллельны и лежат в одной плоскости SBN (так как они опущены на апофему SN). Треугольники SHL и SH1B подобны и LH/BH1=SL/SB, угол KSQ равен углу ASC и равен α. Тогда объем пирамиды LKSQ относится к объему пирамиды ВASC:
Vlksq/Vbasc = (1/3)*LH*Sksq/(1/3)*BH1*Sasc = (SL/SB)*[(KS*SQ*sinα)/(AS*SC*sinα)] = (SL*KS*SQ)/(SB*AS*SC), что и требовалось доказать.
Осталось найти SQ. Соединим К и N. KN - средняя линия треугольника ASC (так как AN=NC и AK=KS - дано). KN параллельна SC. Треугольник SMQ подобен треугольнику NMK по двум углам: <SMQ=<KMN (вертикальные), а <SQM=<MKN (внутренние накрест лежащие при параллельных KN и SC и секущей KQ).
Тогда SQ/KN=SM/MN. Но SM/MN=SL/LB (так как треугольник MSL подобен треугольнику NSB (ML параллельна NB). Имеем:
SM/MN=SL/LB = (1/3):(2/3) = 1/2. Тогда SQ = (SM/MN)*KN = (1/2)*(b/2) = (1/4)*b,
где b - ребро данной нам пирамиды (AS=BS=CS=b).
Вставим имеющиеся данные в доказанное выше соотношение и получим:
Vlksq/Vbasc = (SL*KS*SQ)/(SB*AS*SC)= [(b/3)*(b/2)*(b/4)]/(b*b*b) = 1/24.
Тогда объем нижней части пирамиды равен Vsabc-Vlksq = 1-1/24 = 23/24 объема пирамиды SABC.
Отсюда объем нижней части пирамиды (находящейся под плоскостью сечения) равен (23/24)*Vbasc=(23/24)*48 = 46.
Ответ: объем части пирамиды, лежащей ниже плоскости cечения равен 46.
прямой BN. Для этого надо через точку L провести прямую LM, параллельную BN. Тогда прямые KL и LM определяют нужную нам плоскость сечения. Проведем прямую SN (апофему грани ASC). Прямая LM пересекает SN в точке M, так как LM и BN лежат в одной плоскости NSB. Продолжим КМ до пересечения с SC в точке Q. Плоскость KLQ - плоскость искомого сечения.
Теперь надо найти объем пирамиды SКLQ, вычесть его из объема пирамиды SABC (48) и получим ответ.
Известно, что объемы тетраэдров, имеющих равные трехгранные углы, относятся как произведения длин ребер, образующих эти углы. Наша пирамида правильная, значит трехгранные углы при вершине S равны.
Докажем правильность данного выше утверждения для нашего случая.
Проведем высоты LH и BH1 в пирамидах LKSQ и ВASC. LH и BH1 параллельны и лежат в одной плоскости SBN (так как они опущены на апофему SN). Треугольники SHL и SH1B подобны и LH/BH1=SL/SB, угол KSQ равен углу ASC и равен α. Тогда объем пирамиды LKSQ относится к объему пирамиды ВASC:
Vlksq/Vbasc = (1/3)*LH*Sksq/(1/3)*BH1*Sasc = (SL/SB)*[(KS*SQ*sinα)/(AS*SC*sinα)] = (SL*KS*SQ)/(SB*AS*SC), что и требовалось доказать.
Осталось найти SQ. Соединим К и N. KN - средняя линия треугольника ASC (так как AN=NC и AK=KS - дано). KN параллельна SC. Треугольник SMQ подобен треугольнику NMK по двум углам: <SMQ=<KMN (вертикальные), а <SQM=<MKN (внутренние накрест лежащие при параллельных KN и SC и секущей KQ).
Тогда SQ/KN=SM/MN. Но SM/MN=SL/LB (так как треугольник MSL подобен треугольнику NSB (ML параллельна NB). Имеем:
SM/MN=SL/LB = (1/3):(2/3) = 1/2. Тогда SQ = (SM/MN)*KN = (1/2)*(b/2) = (1/4)*b,
где b - ребро данной нам пирамиды (AS=BS=CS=b).
Вставим имеющиеся данные в доказанное выше соотношение и получим:
Vlksq/Vbasc = (SL*KS*SQ)/(SB*AS*SC)= [(b/3)*(b/2)*(b/4)]/(b*b*b) = 1/24.
Тогда объем нижней части пирамиды равен Vsabc-Vlksq = 1-1/24 = 23/24 объема пирамиды SABC.
Отсюда объем нижней части пирамиды (находящейся под плоскостью сечения) равен (23/24)*Vbasc=(23/24)*48 = 46.
Ответ: объем части пирамиды, лежащей ниже плоскости cечения равен 46.
Приложения:
Ответил Matilda1212
0
Большое Вам спасибо. Доступно и доходчиво.
Ответил IUV
0
эскизы к задаче во вложении
решение не выкладываю - все уже решено
решение не выкладываю - все уже решено
Приложения:
Новые вопросы