в правильной треугольной пирамиде боковое ребро равно 9 см, высота - 6 см. Найдите длину стороны основания

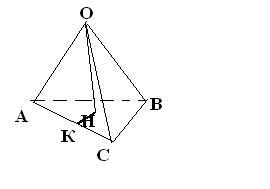
Треугольник АОН-прямоугольный, угол ОНА=90 градусов, т.к. ОН-высота.

По теореме Пифагора найдём АН:

Т.к. у нас дана правильная пирамида, то в основании лежит правильный треугольник, т.е. равносторонний. Тогда HА-будет биссектриссой угла А.Следовательно угол HAC=30. Проведем перпендикуляр HK на АС. В треугольнике HAK, AK=AH*cos30=

 AK=AC