В правильной четырехугольной пирамиде все ребра равный 10. Найдите объем шара, вписанного в нее
Ответы на вопрос
Объём шара определён формулой: .
Шар можно вписать в любую правильную пирамиду. Центр шара лежит на высоте пирамиды и совпадает с центром окружности, вписанной в равнобедренный треугольник, боковой стороной которого является апофема пирамиды, а высотой - высота пирамиды. Радиус шара равен радиусу этой окружности.
Радиус шара R, высота пирамиды H и радиус окружности r, вписанной в основание пирамиды, связаны соотношением:
Радиус основания r = AD/2 = 10/2 = 5. Высота пирамиды H определим по теореме Пифагора из треугольника SO₁E, предварительно вычислив апофему SE
Из заданного соотношения найдём радиус шара
Объём шара:
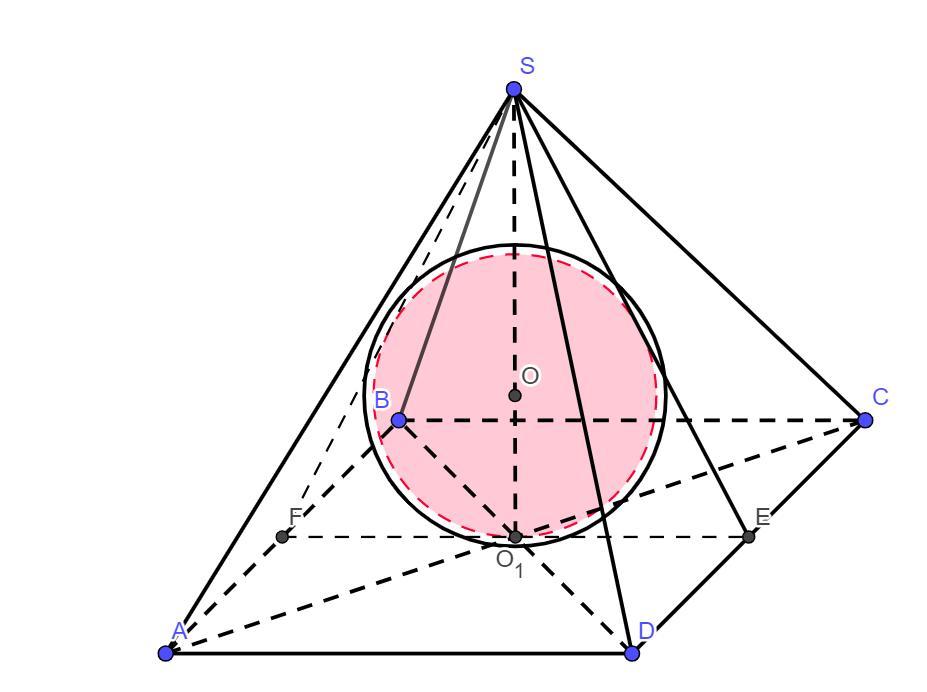
В правильной четырехугольной пирамиде все ребра равный 10. Найдите объем шара, вписанного в нее.
Объяснение:
Шар вписан в правильную пирамиду ⇒ касается боковых граней.
В сечении , проходящем через высоту пирамиды и апофемы противоположных боковых граней , лежит равнобедренный треугольник с вписанным кругом. Центр круга лежит на высоте пирамиды, высоте равнобедренного ΔМРК . Радиус шара равен радиусу вписанного круга.
V= , R=OP=ОМ.
Т.к. все ребра равны 10 ед, то из ΔАВС по т. Пифагора АС=√(10²+10²)=10√2 ⇒ АО= 5√2 по свойству диагоналей квадрата.
Тогда из прямоугольного ΔАЕМ , МЕ=√(10²-(5√2)² )=√(100-50)=5√2 .
ΔРОЕ -прямоугольный , ОЕ=МЕ-МО , ОЕ=5√2-R. Тогда по т. Пифагора РО²=ОЕ²+РЕ² или
R²=(5√2-R)²+5²
R²=25*2-2*5√2*R+R²+25,75
10√2R=75 ⇒ R=7,5/√2.
V= =
=
=
V=140,625√2*π ед³ или
V= ед³ .
