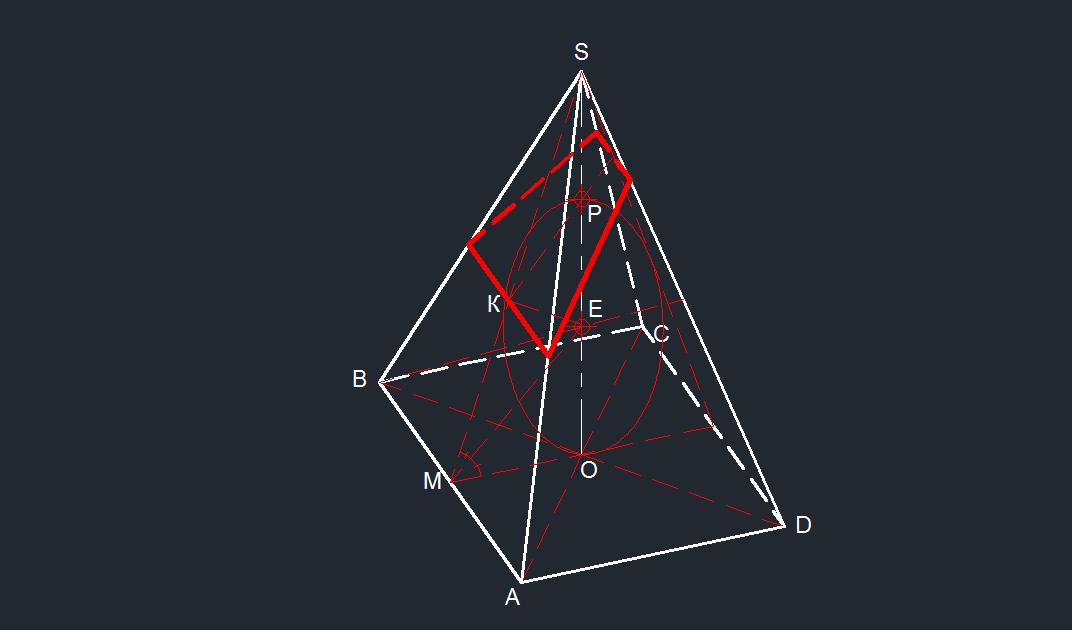
в правильной четырехугольной пирамиде SABDC длина высоты , опущенной из вершины Ы на соснование ABCD, равна 6√2. Через точкукасания с боковой гранью SAB вписанного в эту пирамиду шара параллельно прямой AB проведена плоскость , проходящая через ближайшую к вершине S точку шара.
а)постройте сечение пирамиды этой плоскостью
б)найдите площадь сечения,если AB=4√6
Ответы на вопрос
Ответил dnepr1
0
Угол наклона боковых граней α = arc tg H / (a/2) = 6√2 / (4√6/2) =
= arc tg 3√(1/3) = arc tg√3 = 60°.
Центр сферы находится на пересечении биссектрис углов, образованных апофемами боковых граней и плоскостью основы.
Проведём вертикальную секущую плоскость через ось пирамиды и апофему. Линии сечения этой плоскостью основы и боковых граней образуют равносторонний треугольник со стороной 4√6.
Радиус окружности в сечении сферы равен r = (a/2)*tg (60/2) =
= 2√6*(1/√3) = 2√2.
Точка К касания находится на расстоянии r/tg 30 = 2√2 / (1/√3) = 2√6 - это середина апофемы.
Плоскость наклонена под углом 30 градусов к основе.
В сечении получается трапеция. Нижнее основание её равно 1/2 стороны квадрата основы, а верхнее 1/4 части.
Высота трапеции равна 2√6*cos 30 = 2√6*(√3/2) = √18 = 3√2.
Площадь S = ((2√6+√6)/2)*3√2 = 9√3.
Общий вид и сечение показаны в приложении.
= arc tg 3√(1/3) = arc tg√3 = 60°.
Центр сферы находится на пересечении биссектрис углов, образованных апофемами боковых граней и плоскостью основы.
Проведём вертикальную секущую плоскость через ось пирамиды и апофему. Линии сечения этой плоскостью основы и боковых граней образуют равносторонний треугольник со стороной 4√6.
Радиус окружности в сечении сферы равен r = (a/2)*tg (60/2) =
= 2√6*(1/√3) = 2√2.
Точка К касания находится на расстоянии r/tg 30 = 2√2 / (1/√3) = 2√6 - это середина апофемы.
Плоскость наклонена под углом 30 градусов к основе.
В сечении получается трапеция. Нижнее основание её равно 1/2 стороны квадрата основы, а верхнее 1/4 части.
Высота трапеции равна 2√6*cos 30 = 2√6*(√3/2) = √18 = 3√2.
Площадь S = ((2√6+√6)/2)*3√2 = 9√3.
Общий вид и сечение показаны в приложении.
Приложения:
Новые вопросы