В правильной четырехугольной пирамиде плоский угол при вершине равен углу между боковым ребром и ребром основания. Определите двугранный угол при боковом ребре пирамиды, зная, что плоский угол при вершине равен 60°.

Боковые грани заданной пирамиды - правильные треугольники.

Основание - квадрат со стороной, равной стороне боковой грани.

Примем длины всех рёбер, равными 1.

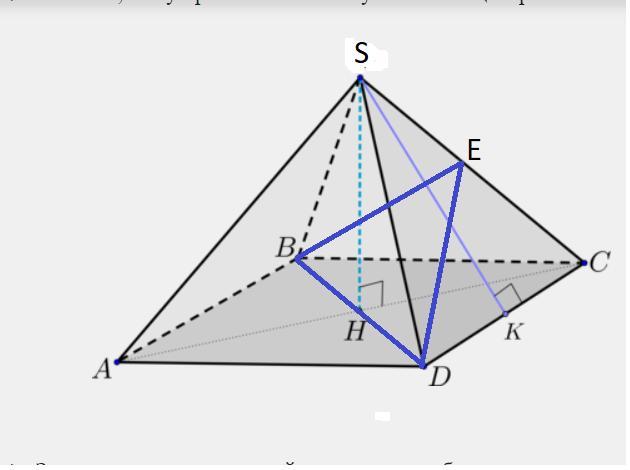
Искомый угол - это угол между высотами ВЕ и ЕD к боковому ребру.

ВЕ = ЕD = 1*cos 30 = √3/2.

Диагонаь основания BD = √2.

Угол находим по теореме косинусов.

cos φ = ((√3/2)² + (√3/2)² - (√2)²)/(2*(√3/2)*(√3/2)) =

          = ((3/4) + (3/4) - 2)/(2*(3/4)) = (6/4) - 2)/(6/4)  =

          = (-1/2)/(3/2) = -1/3.

Ответ: двугранный угол при боковом ребре пирамиды равен

           arccos(-1/3) ≈ 109,4712°.