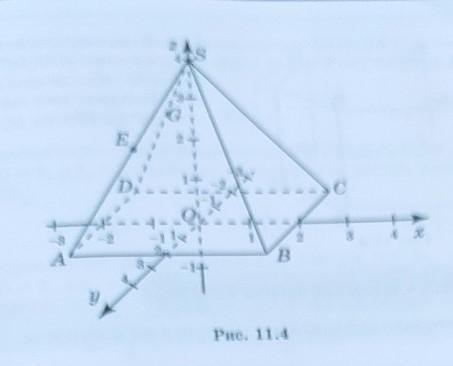
В правильной четырехугольной пирамиде CABCD стороны основания и высота равны 4 см. Точка Е - середина ребра СА ( рис. 11.4 ) . Найдите расстояние от точки Е до плоскости SBC .
РЕШИТЕ ПОЖАЛУЙСТА С ОБЪЯСНЕНИЕМ, очень нужно до ЗАВТРА
Приложения:
Ответы на вопрос
Ответил au456
6
Условие конечно неверно записано, но благо из рисунка все понятно ))
Оси на нем обозначены.
Координаты точек
Е (-1;1;2)
S(0;0;4)
B(2;2;0)
C(2;-2;0)
Уравнение плоскости SBC
ax+by+cz+d=0
Подставляем координаты точек S B C
4c+d=0
2a+2b+d=0
2a-2b+d=0
Откуда b =0
Пусть d = -4 , тогда с=1, а =2
Искомое уравнение
2х+z-4 =0
k = √(2^2+1^2)=√5
Нормальное уравнение плоскости
2x/√5+z/√5-4/√5 =0
Для нахождения искомого расстояния подставляем координаты точки Е в нормальное уравнение плоскости
| Е; SBC | = | -2/√5+2/√5-4/√5 | = 4/√5
lizasembaeva563:
большое спасибо
Помогите, пожалуйста с геометрией. Задачи в моем профиле.
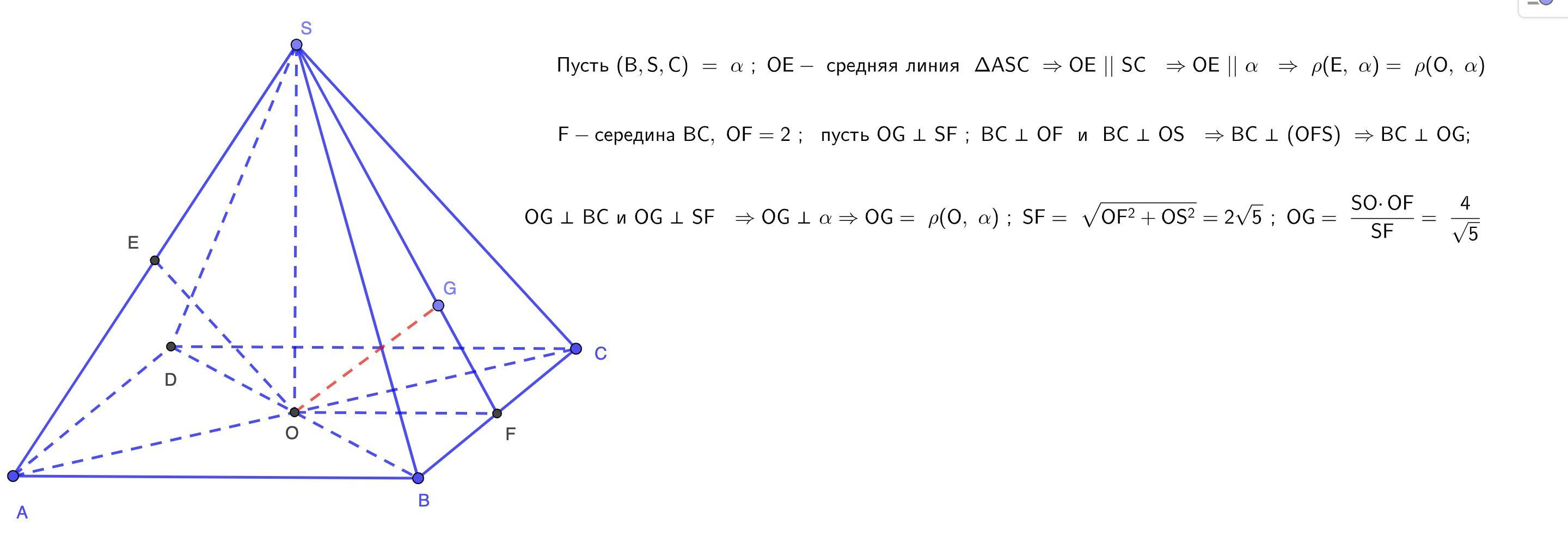
Спасибо за решение. Если решать чисто геометрически (сплошной Пифагор), то решение, на мой взгляд, проще. Результат тот же : h = (4√5)/5.
Это рисовать надо ) А ведь есть же люди которые только котов рисовать умеют )) Им тоже надо геометрию сдавать ....
Ответил antonovm
6
Ответ:
4 / √5 ...........
Объяснение:
Приложения:
помогите пожалуйста разобраться
Новые вопросы
Қазақ тiлi,
1 год назад
Українська мова,
6 лет назад
Русский язык,
6 лет назад
Математика,
8 лет назад