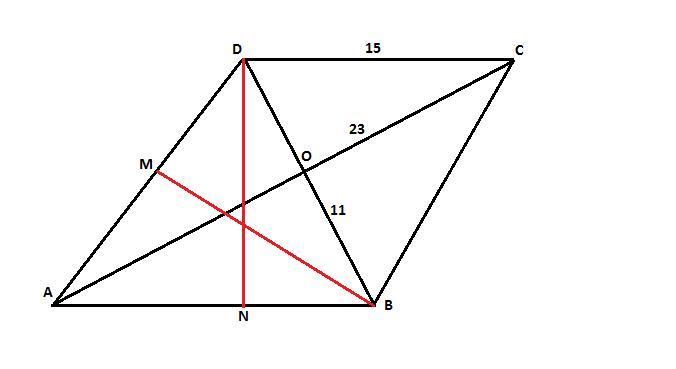
В параллелограмме с диагоналями 23 и 11 известна сторона - 15.
Найдите : 1. другую сторону параллелограмма
2. площадь параллелограмма
3. высоты параллелограмма
Ответы на вопрос
Ответ:
1) BC = 10 см; 2) S(ABCD) = 24√21 см^2;
3) BM = 2,4√21 см; DN = 1,6√21 см.
Объяснение:
Смотрите рисунок. Параллелограмм ABCD.
Диагонали AC = 23 см, BD = 11 см. Сторона AB = CD = 15 см.
Найти:
1) Другую сторону BC = AD.
2) Площадь параллелограмма S(ABCD).
3) Высоты параллелограмма BM и DN.
Решение:
1) Есть такое свойство диагоналей параллелограмма:
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
AC^2 + BD^2 = 2(AB^2 + BC^2)
Отсюда:
BC^2 = (AC^2 + BD^2)/2 - AB^2 = (23^2 + 11^2)/2 - 15^2
BC^2 = (529 + 121)/2 - 225 = 650/2 - 225 = 325 - 225 = 100
BC = AD = √100 = 10 см.
2) Площадь параллелограмма ABCD в 2 раза больше площади треугольника ABD. А его можно найти по формуле Герона:
P(ABD) = AB + AD + BD = 15 + 10 + 11 = 36 см
p = P(ABD)/2 = 36/2 = 18 см.
см^2
S(ABCD) = 2*S(ABD) = 2*12√21 = 24√21 см^2
3) С другой стороны, площадь параллелограмма можно найти так:
S(ABCD) = AB*DN = AD*BM
Отсюда высоты параллелограмма:
BM = S(ABCD)/AD = 24√21/10 = 2,4√21 см.
DN = S(ABCD)/AB = 24√21/15 = 1,6√21 см.