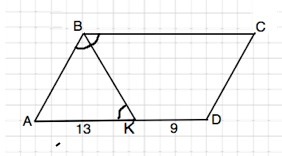
В параллелограмме АВСД биссектриса тупого угла делит противоположную сторону на отрезки 13 и 9. Найдите периметр параллелограмма.
Ответы на вопрос
Ответил Hrisula
0
АBCD параллелограмм, ⇒ его противоположные стороны равны и параллельны. При пересечении параллельных прямых секущей накрестлежащие углы равны. Секущая ВК пересекает ВС и АD, следовательно, накрестлежащие ∠СВК=∠АКВ. В то же время ВК, как биссектриса, делит угол АВС пополам, следовательно, ∠АВК=∠СВК.⇒ ∠АКВ=∠АВК.
Углы при основании ВК Δ ВАК равны, ⇒ он равнобедренный, и ВА=КА=13
Полупериметр АВСD=АВ+АК+КD=35, периметр=35•2=70 (ед. длины).
Приложения:
Новые вопросы
Геометрия,
1 год назад
Математика,
1 год назад
Алгебра,
7 лет назад
Математика,
7 лет назад
Математика,
8 лет назад