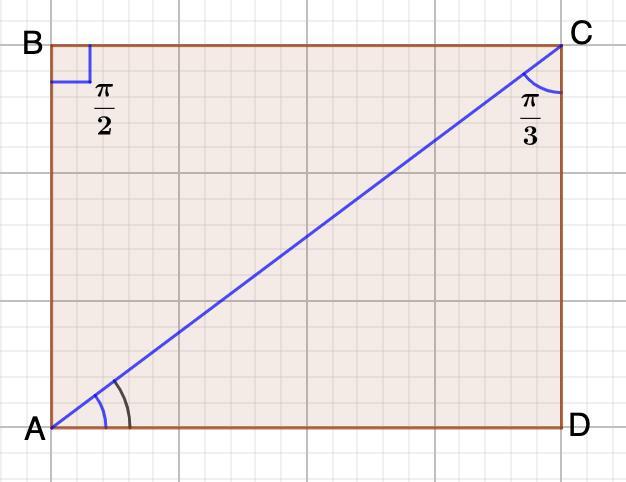
В параллелограмме ABCD угол В= П/2, угол ACD=П/3. Найти sin угла CAD.
СРОЧНО, ДАЮ 40 БАЛЛОВ

Ответ:

Синус угла CAD равен .

Пошаговое объяснение:

Требуется найти sin угла CAD.

Дано: ABCD - параллелограмм;

∠В = ; ∠ACD = ;

Найти: sin∠CAD.

Решение:

1. Переведем данные значения углов в градусы:

2. Рассмотрим ABCD - параллелограмм.

∠В = 90° (условие)

• Противоположные углы параллелограмма равны.

⇒ ∠В = ∠D  = 90°

3. Рассмотрим ΔАСD - прямоугольный.

• Сумма острых уголов прямоугольного треугольника равна 90°.

⇒ ∠CAD = 90° - ∠ACD = 90° - 60° = 30°

По таблице найдем:

Синус угла CAD равен .