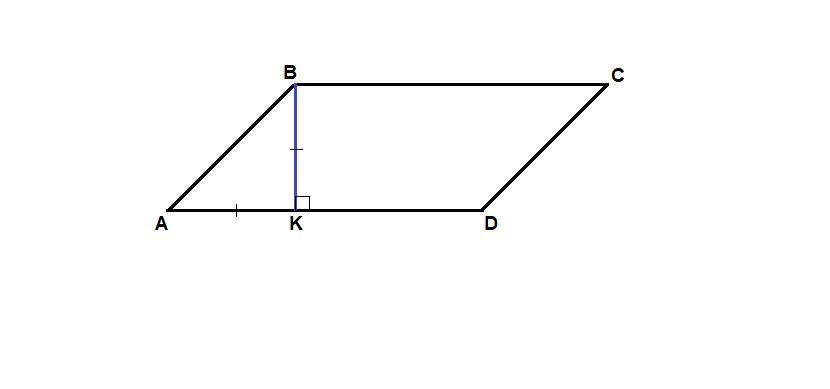
В параллелограмме ABCD с острым углом A из вершины B опущен перпендикуляр BK к прямой AD, AD=BK. Найти угол C и угол D.

Ответ:

∠C = 45°,   ∠D = 135°

Объяснение:

В условии ошибка. Должно быть так:

В параллелограмме ABCD с острым углом А из вершины B опущен перпендикуляр BK к прямой AD, AК равно BK.  

Найдите угол C, угол D.

Треугольник АВК равнобедренный с основанием АВ, ∠АКВ = 90°, значит ∠КАВ = ∠КВА = (180° - 90°)/2 = 45°.

Противолежащие углы параллелограмма равны, значит

∠С = ∠КАВ = 45°.

Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°, значит

∠D = 180° - ∠C = 180° - 45° = 135°