В параллелограмме abcd биссектриса острого угла bcd пересекает сторону ad в точке m, а продолжение стороны AB в точке K, KM:KC = 2:3
а) Докажите, что треугольники KAM и CDM подобны
б) найдите стороны параллелограма abcd, если его периметр равен 48 см

Ответ:

6 см, 18 см

Объяснение:

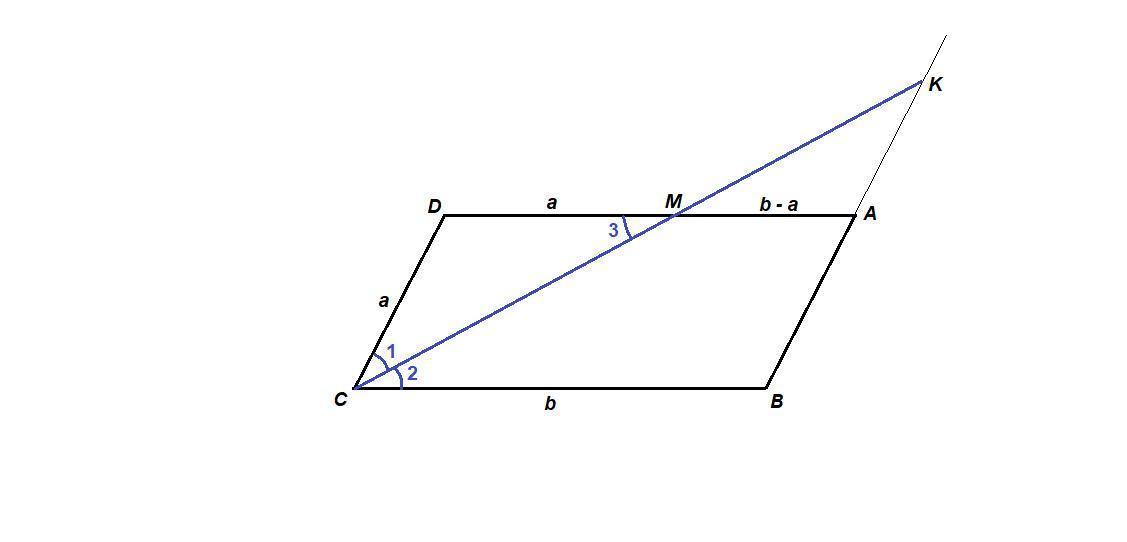
ABCD -  параллелограмм,

АВ = CD = a

AD = BC = b

Pabcd = 2(a + b) = 48 cм

a + b = 24                    (1)

∠2 = ∠1 так как CM биссектриса,

∠2 = ∠3 как накрест лежащие при пересечении параллельных прямых AD и ВС секущей CM, значит

∠1 = ∠3 и значит ΔCDM равнобедренный с основанием CM.

CD = DM = а,  ⇒  MA = b - a.

ΔKAM ~ ΔCDM по двум углам (углы при вершине М равны, как вертикальные, ∠KАМ = ∠CDM как накрест лежащие при пересечении параллельных прямых AВ и CD секущей AD), следовательно

KM : KC = 2 : 3,   ⇒   KM : MC = 2 : 1

b - a = 2a

b = 3a

С учетом уравнения (1) получаем систему уравнений:

AB = 6 см

ВС = 18 см