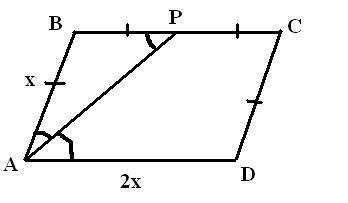
в паралелограмме ABCD бессектриса угла А пересекает сторону ВС в точке Р так что ВР = РС. Найдите стороны паралелограмма если периметр равен 42 см.

Треугольник АВР - равнобедренный, т. к. угол ВРА = углу РАD, как накрест лежащие, а угол ВАР = углу РАD, т. к. АР - биссектриса и делит угол А на два равных угла. Значит АВ = ВР, а ВР = РС по условию, зачит АВ = ВР = РС, зная это мы можем составить уравнение:
2х + 2х + х + х = 42
6х = 42
х = 7 - см стороны АВ и СD
7 * 2 = 14 см - стороны ВС и АD