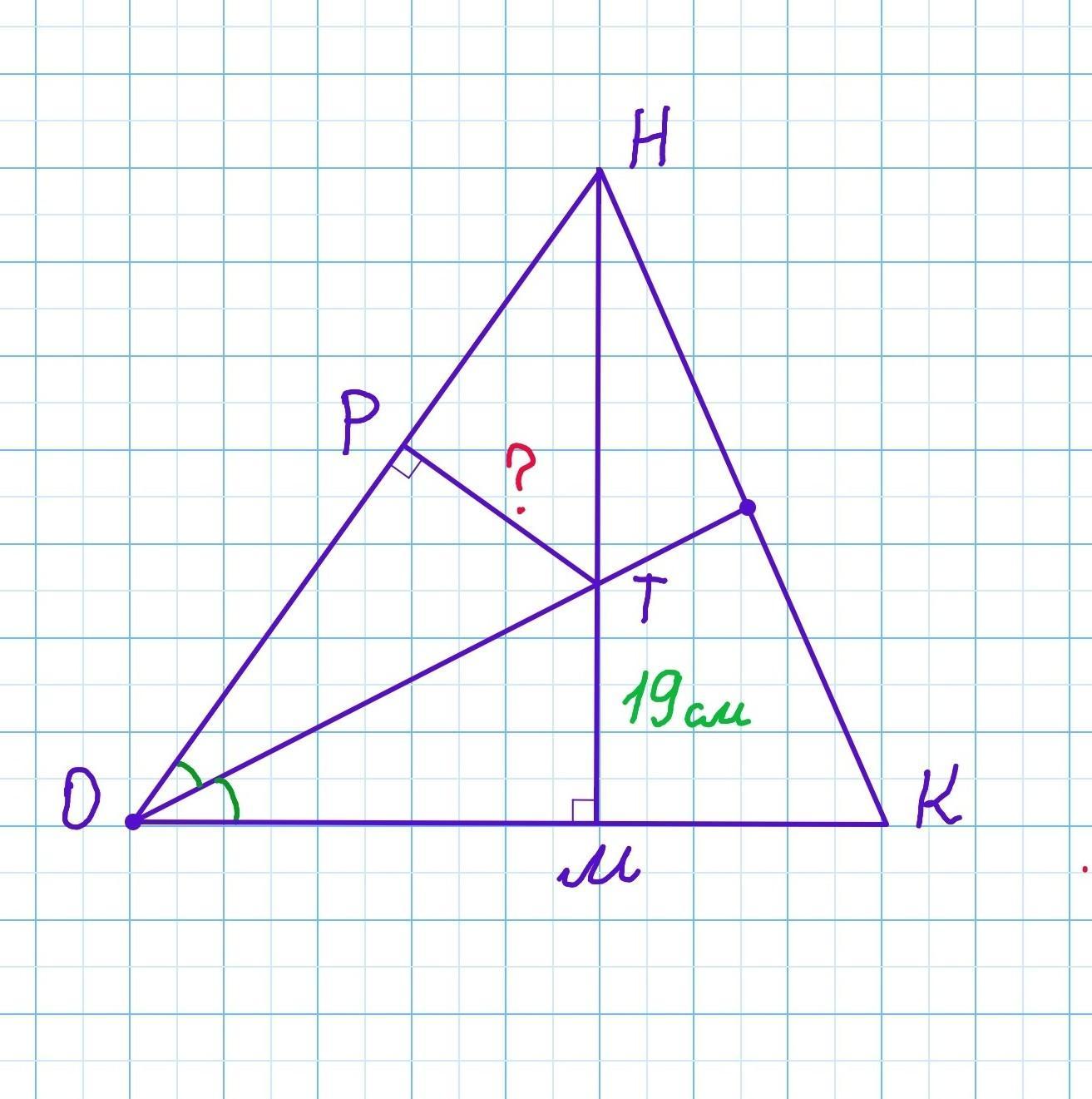
В остроугольном треугольнике ОНК
биссектриса угла О пересекает высоту НМ в
точке Т, причем ТМ= 19 см. Найдите
расстояние от точки Т до прямой ОН.
Ответы на вопрос
Ответил ReMiDa
2
Ответ:
Расстояние от точки Т до прямой ОН равно 19 см.
Объяснение:
Дан остроугольный треугольник ОНК. Биссектриса угла О пересекает высоту НМ в точке Т, причем ТМ= 19 см. Найдите расстояние от точки Т до прямой ОН.
Расстояние от точки до прямой равно длине перпендикуляра, опущенного из точки на прямую.
Проведём ТР⟂ОН. △ОТР - прямоугольный (∠Р=90°).
Так как HM - высота, то △ОТМ также прямоугольный (∠М=90°).
△ОТР=△ОТМ по гипотенузе и острому углу. Действительно, ∠РОТ=∠МОТ, так как ОТ - биссектриса, гипотенуза ОТ - общая.
Из равенства треугольников следует равенство сторон: ТР=ТМ=19 см
С другой стороны, по определению биссектрисы угла:
Любая точка, лежащая на биссектрисе угла, равноудалена от сторон данного угла. Значит ТР=ТМ=19 см.
Приложения:
Новые вопросы