В остроугольном треугольнике ABC AB:AC=√165, а продолжение медианы AM и биссектриса внешнего угла треугольника при вершине C пересеклись в точке K. Через точку K проведена прямая KQ||AC так, что Q – точка пересечения KQ с прямой BC. Также на луче AC отмечена точка L, причём CL:KL:KQ=7:
. Синус угла B равен 1/13. Найдите отношение радиусов окружностей, описанных около треугольников QCL и CKL, а также отношение площади CQKL к площади треугольника QCL.
siestarjoki:
калькулятор или таблицы Брадиса, arcsin(0,988)=81°6'=81,15°
Понял!
Я решил Ваше задание, но у меня всё равно получается решение на 20 страниц. Не знаю что делать!
Я думал найти как-то радиус описанной окружности через теорему синусов.
Но так не получилось!
Всё равно приходится использовать теорему косинусов
Для теоремы синусов нужен хотя-бы один угол. Здесь углов - 0!!
Или есть угол, но не тот который надо!
Я не знаю что с этим делать, это не задачу, а одни расстройства - весь день потратил!
Если у кого-то будут какие-то идеи - пишите.
Ответы на вопрос
Ответил teacherGeometrie
2
Ответ:
Я решил Ваше задание
Объяснение:
Приложения:
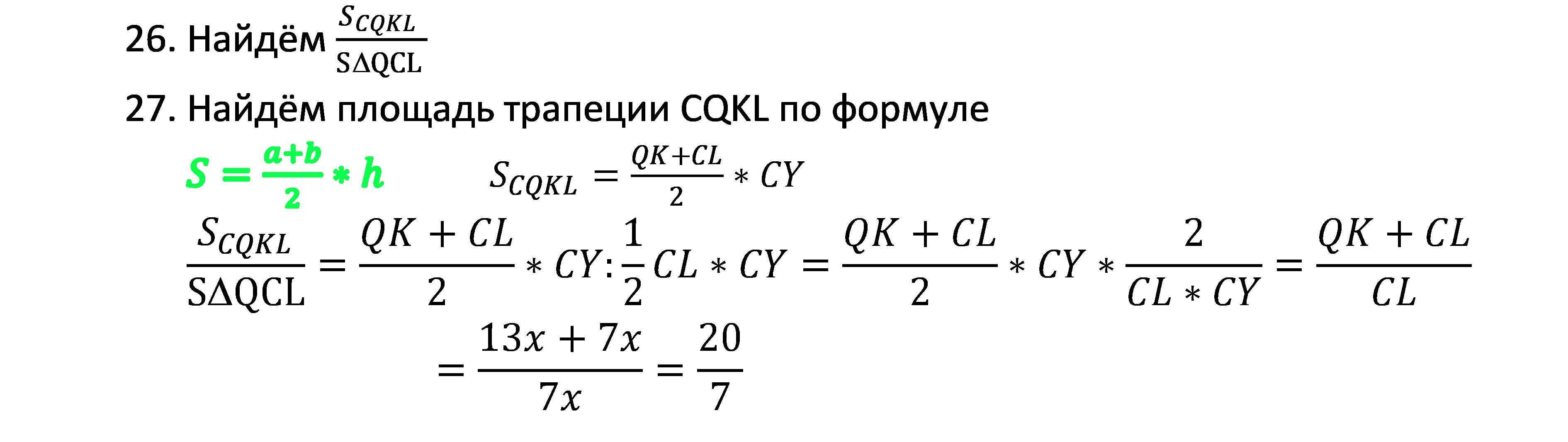
Ответил siestarjoki
1
Ответ:
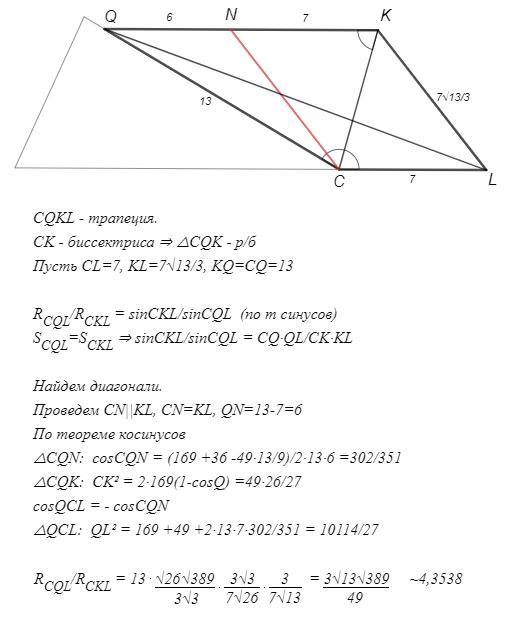
R CQL /R CKL = 3√13√389 /49 ~4,3538
S CQKL/S QCL =20/7
Объяснение:
Дана трапеция CQKL с тупым углом С. Диагональ CK является биссектрисой, отсекает равнобедренный треугольник.
Треугольники QKL и QCL имеют равные высоты, следовательно их площади относятся как основания.
S QKL/S QCL =KQ/CL =13/7
S CQKL/S QCL = S QKL+S QCL / S QCL =20/7
Приложения:
Новые вопросы