В основании пирамиды SABCD лежит квадрат со стороной, равной 5. Точка М делит ребро SB в отношении 2:3, считая от точки S. Через точку М проходит сечение, параллельное основанию пирамиды. найдите его площадь
Ответы на вопрос
Ответил M0nstrodamus
0
поскольку сечение у нас не будет изменяться в зависимости от углов и высоты пирамиды, то мы можем разделить её ребро на 5 равных отрезков и проводить их через пропорцию, то есть при максимальной длине равной 5ти отрезкам, длина стороны основания будет равна 5, а при 0, то есть в вершине пирамиды площадь сечения так же нулевая. Беря два отрезка от вершины, мы получаем длину стороны основания равную 2 и, при условии, что основание квадратной формы, мы получаем площадь сечения равную 4.
Ответил Hrisula
0
Так как основание пирамиды квадрат, параллельное ему сечение тоже квадрат.
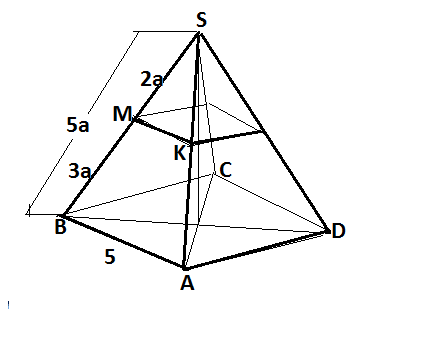
Пусть SM=2а, МВ=3а, тогда SB=5а.
Треугольники SAB и SKM подобны. т.к МК параллельна АВ и углы при основаниях равны как соответственные при пересечении параллельных прямых секущими, и угол S-общий.
Коэффициент подобия = SМ:SВ
k=2а:5а=2/5 АВ⇒
МК=2.
S сечения =2²=4 ед. площади.
Пусть SM=2а, МВ=3а, тогда SB=5а.
Треугольники SAB и SKM подобны. т.к МК параллельна АВ и углы при основаниях равны как соответственные при пересечении параллельных прямых секущими, и угол S-общий.
Коэффициент подобия = SМ:SВ
k=2а:5а=2/5 АВ⇒
МК=2.
S сечения =2²=4 ед. площади.
Приложения:
Новые вопросы