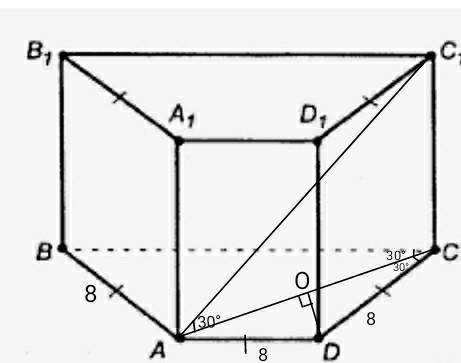
в основі прямої призми лежить рівнобічна трапеція з гострим кутом 60 і меншою основою 8 см. Діагоналі трапеції є бісектрисами її гострих кутів. Знайдіть площу бічної поверхні призми, якщо діагоналі призми утворюють з основою кут 30*

Ответ:

320см²

Объяснение:

Якщо діагоналі трапеції є бісектрисами гострих кутів, тоді меньша основа дорівнює боковій стороні.

AD=AB=DC=8см.

∆ADC- рівнобедрений трикутник.

ОD- висота трикутника ∆АDC.

AO=OC.

∠OAD=30°

OD=AD/2=8/2=4см.

∆АОD- прямокутний трикутник.

За теоремою Піфагора:

АО=√(АD²-OD²)=√(8²-4²)=4√3 см

АС=2*АО=2*4√3=8√3см.

∆ВАС- прямокутний трикутник.

ВА=8 см, катет проти кута 30°;

ВС=2*ВА=2*8=16см.

Р(ABCD)=BC+3*AB=16+3*8=16+24=40см.

∆С1АС- прямокутний трикутник.

tg∠C1AC=CC1/AC

tg30°=1/√3

1/√3=CC1/8√3

CC1=8√3/√3=8 см

Sбіч=Р(ABCD)*CC1=40*8=320см²