В окружности с центром О через середину радиуса проведено хорду АВ, перпендикулярную к нему. Найдите угол АОВ

Ответ:

∠AOB = 120°.

Объяснение:

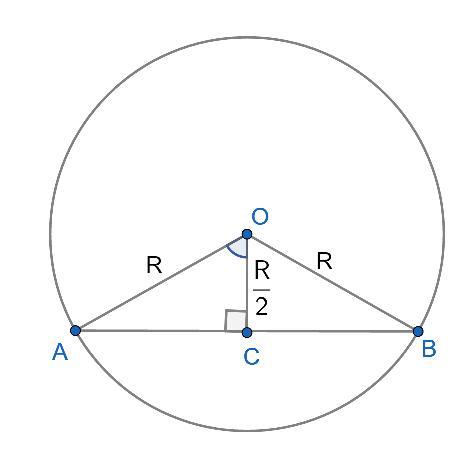
Рисунок прилагается.

ΔAOB равнобедренный, так как AO = OB = R.

По условию т.C - середина радиуса ⇒ OC = R/2

По условию AB ⊥ OC.

В равнобедренном ΔAOB перпендикуляр ОС является высотой, медианой и биссектрисой.

Тогда  ∠AOC = ∠AOB/2;

ΔAOC прямоугольный, ∠ACO = 90°, AO - гипотенуза, OC и AС катеты.

Косинус угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе.

∠AOB = 2 * ∠AOC = 2 * 60° = 120°.