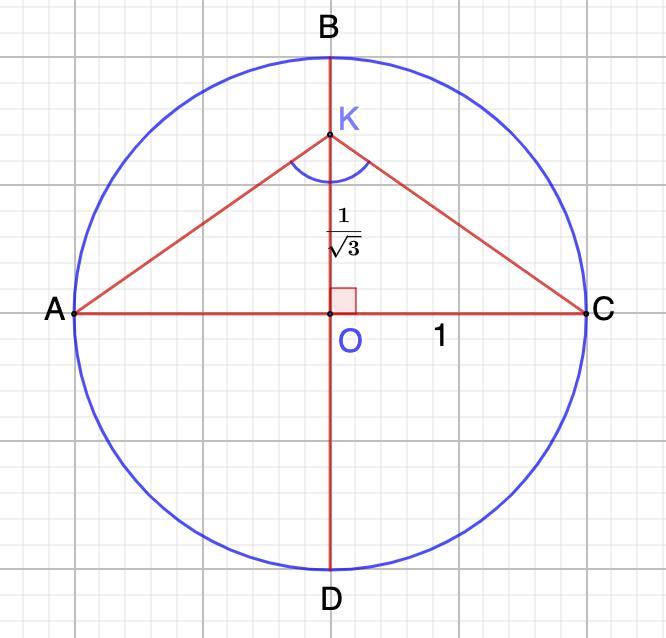
В окружности радиус которой равен 1 проведены два заимно перпендикулярных диаметра АС и ВД пересекающиеся в точке О . найдите угол АКС где К лежит на радиусе ОВ и ОК = 1/корень3 ответ в градусах

Ответ:

120°

Пошаговое объяснение:

Дано: Окр.О,ОС.

АС ⊥ BD  - диаметры;

К ∈ ОВ;

Найти: ∠АКС

Решение:

1. Рассмотрим ΔАКС - прямоугольный.

• Тангенс угла - отношение противолежащего катета к прилежащему.

⇒ ∠ОКС = 60°

2. Рассмотрим ΔАКО и ΔОКС - прямоугольные.

АО = ОС = R; ОК - общая.

⇒ ΔАКО = ΔОКС (по двум катетам)

• В равных треугольниках против равных сторон лежат равные углы.

⇒ ∠АКО = ∠ОКС = 60°

∠АКС = 60°+60° = 120°