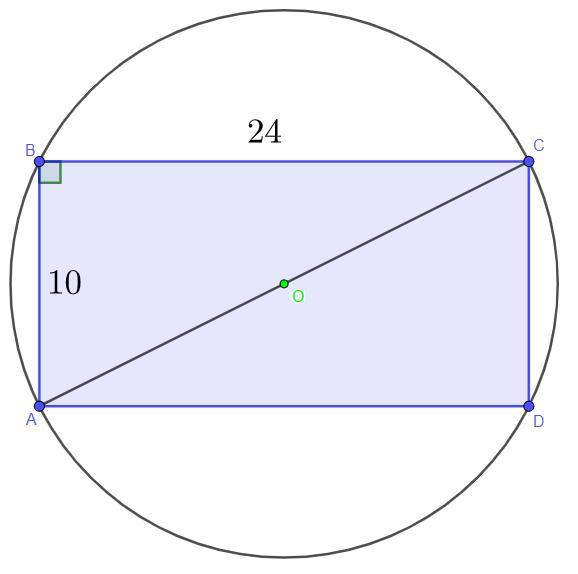
В окружность вписан прямоугольник со сторонами 24 и 10. Найдите длину окружности.

Можете в тетради все написать и скинуть пожалуйста​

Ответ:

Длинна окружности равна 26π

Примечание:

Длинна окружности: L = πD

• L - длина окружности

• D - диаметр окружности

Объяснение:

Дано: ABCD - вписанный прямоугольник, BC = 24, AB = 10

Найти: L - ?

Решение:

Так как по условию ABCD - прямоугольник, то по свойствам прямоугольника все его углы равны 90°, тогда ∠ABC = 90°.

Рассмотрим треугольник ΔABC.

Треугольник ΔABC прямоугольный, так как ∠ABC = 90°.

По теореме Пифагора:

.

По теореме вписанный угол с градусной мерой 90° опирается на диаметр, тогда так по условию окружность описана около прямоугольника ABCD, то AC - хорда окружности и угол ∠ABC = 90° и является вписанным углом, то отрезок AC - диаметр окружности.

По формуле длинны окружности:

• L = πD = 26π.

#SPJ3