В окружность с радиусом 4 корень из 3 см вписан правильный треугольник,

a) найдите сторону треугольника

в)вычислите площадь круга вписанного в этот треугольник​

Ответ:

36π или 113,095

Объяснение:

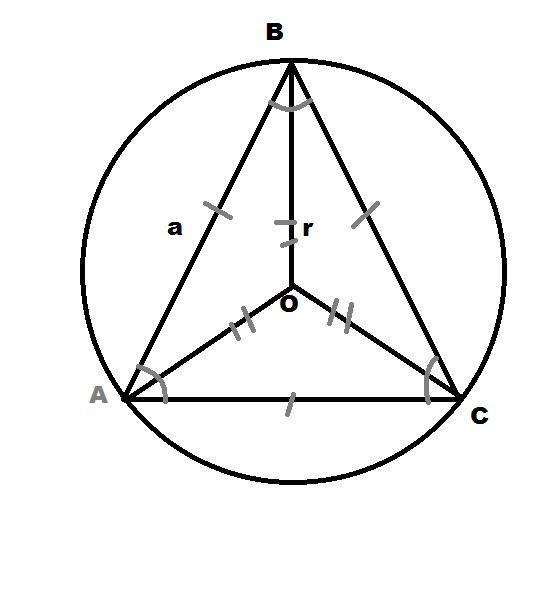
Т.К. треугольник правильный, то центр окружности находится на пересечении биссектрис ⇒ ∠ABO = ∠BAO = 30° ⇒ ∠AOB=180°-∠BAO -∠ABO = 120°

По теореме косинусов

a² = AO²+BO² - 2*AO*OB*cos∠120°=2*48 -48

a=

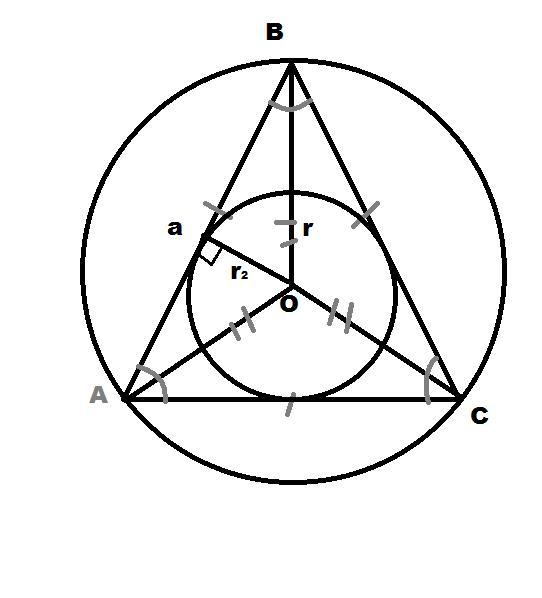
r₂ =√(r₁²- ()²) ==6

S=πr²=36π