В наклонном параллелепипеде авсда1в1с1д1 боковое ребро равно 10. Расстояние между ребром аа1 и ребрами вв1 и дд1 соответственно равны 5 и 12,а расстояние между аа1 и сс1 равно 13.Найдите объем.

В наклонном параллелепипеде авсда1в1с1д1 боковое ребро равно 10. Расстояние между ребром аа1 и ребрами вв1 и дд1 соответственно равны 5 и 12,а расстояние между аа1 и сс1 равно 13. Найдите объем.
Решение.
Параллелепипед - это четырёхугольная призма, все грани которой являются параллелограммами. 
Объем параллелепипеда находят так же, как объем призмы.  
Объем призмы 
V = Sоснh = Sсечl, где Sосн − площадь основания, h − высота призмы, Sсеч − площадь перпендикулярного сечения, l − боковое ребро призмы.
Расстояние между ребром АА1 и ребром ВВ1 равно расстоянию между ребром ДД1 и ребром СС1, так как грани АА1В1В и ДД1С1С равные параллелограммы.
По условию задачи оно равно 5. 
Точно так же равно расстояние между АА1 и ДД1 и ВВ1 и СС1 и равно 12.
Объем данного параллелепипеда можно найти произведением площади его перпендикулярного сечения на боковое ребро. 
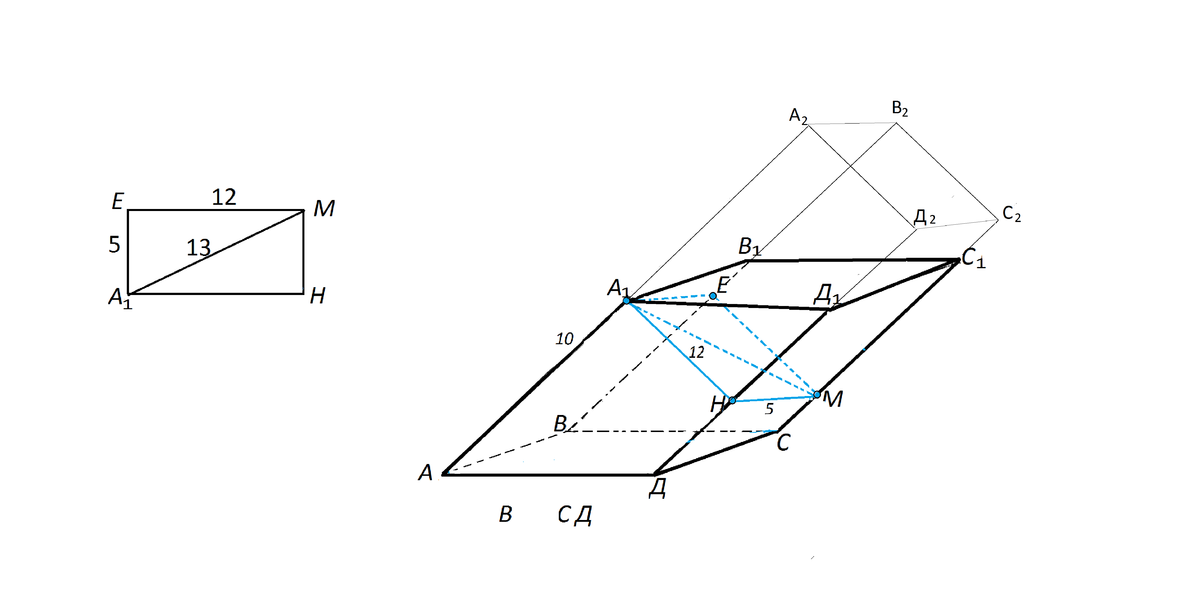
Рассмотрим треугольник А1МН, образованный расстояниями между ребрами. Отношение его сторон равно 12:13:5, и это - отношение сторон  прямоугольного треугольника из Пифагоровых троек ( проверив А1М²=А1Н²+НМ², несложно убедиться в этом). 
Сечение А1ЕМН -прямоугольник.
Следовательно, 
V = Sсечl=А1НМЕ*АА1
 V =12*5*10=600 ед. объема
Так как А1ЕМН -прямоугольник,объем данного параллелепипеда можно найти и произведением площади любой боковой грани на расстояние между нею и противоположной гранью,т.е на высоту параллелепипеда, основанием которого взята именно эта грань.
1) V АВСДА1В1С1Д1=SДСС1Д1*НА1 
2)V АВСДА1В1С1Д1=SАА1Д1Д*НМ
.Нетрудно убедиться, что результат будет тот же, что и в случае нахождения объема через перпендикулярное сечение.  
-------------------
[email protected]