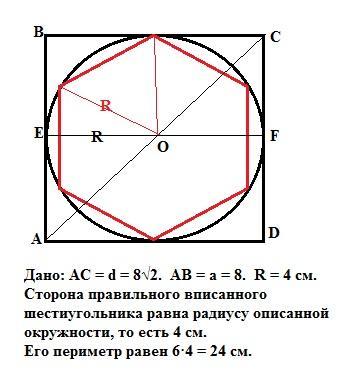
в квадрате с диагональю 8√2 см вписана окружность в которую вписан правильный шестиугольник. найдите его периметр.
Ответы на вопрос
сторона правильного шестиугольника равна радиусу описанной около него окружности, то есть 4 см.
периметр=4х6=24
Ответ: 24 см
Длина окружности равна 12(Пи) см, найдём радиус 2(пи)r=12(пи), r=6 см
длина стороны правильного многоугольника и радиус вписанной окружности связаны формулой а=2r*tg(пи/n)
4/3=2*6*tg(пи/n)
tg(пи/n)=(/3)/3, это угол пи/6 (смотри таблицу значений тангенсов углов), отсюда n=6
Ответ: 6 сторон
Ответ:
Периметр равен 24 см.
Объяснение:
Радиус ВПИСАННОЙ в квадрат окружности равен стороне квадрата. Пусть сторона квадрата равна "а". Тогда по Пифагору квадрат диагонали квадрата : а² + а² = d² или 2а² = 64·2 => а = 8 см.
Значит радиус ваисанной в квадрат окружности равен R = 4см.
У правильного шестиугольника, ВПИСАННОГО в окружность, сторона равна радиусу этой окружности, то есть 4 см.
Тогда периметр шестиугольника равен 6·4 = 24 см.