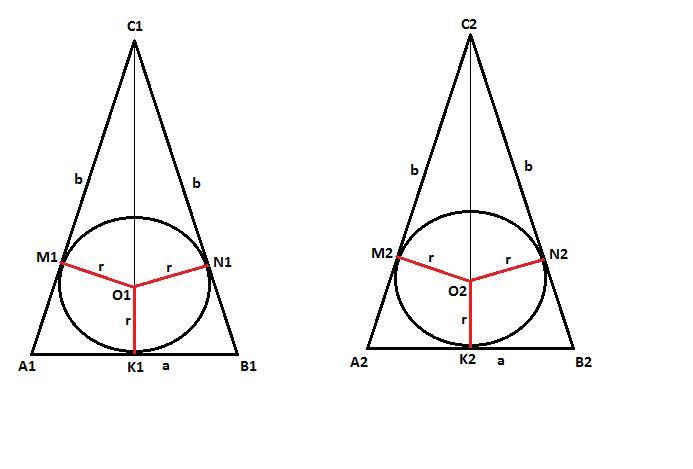
в двух равнобедренных треугольниках равны основания и радиусы вписанных окружностей можно ли утверждать что эти треугольники равны?
чертёж: дано: решение: ответ: ​

Ответ:

Можно

Объяснение:

Дано: два равнобедренных треугольника A1B1C1 и A2B2C2.

Основания равны A1B1 = A2B2 = a.

Радиусы вписанных окружностей тоже равны r1 = r2.

Можно ли утверждать, что треугольники равны?

Решение:

Смотрите рисунок.

Вписанные окружности пересекаются со сторонами треугольников в точках соответственно: (M1; N1; K1) и (M2; N2; K2).

Центры окружностей O1 и O2 находятся на одинаковом расстоянии r от оснований A1B1 и A2B2.

По свойству касательных:

A1M1 = A1K1 = a/2 и A2M2 = A2K2 = a/2

B1N1 = B1K1 = a/2 и B2N2 = B2K2 = a/2

А так как углы тоже одинаковы: A1 = A2 = B1 = B2

То очевидно, что точки C1 и C2 находятся на одинаковом расстоянии от основания: C1K1 = C2K2.

Отсюда и боковые стороны тоже равны:

A1C1 = A2C2 = B1C1 = B2C2 = b

А раз равны и основания, и боковые стороны, то равны и треугольники целиком.

Теорема доказана,