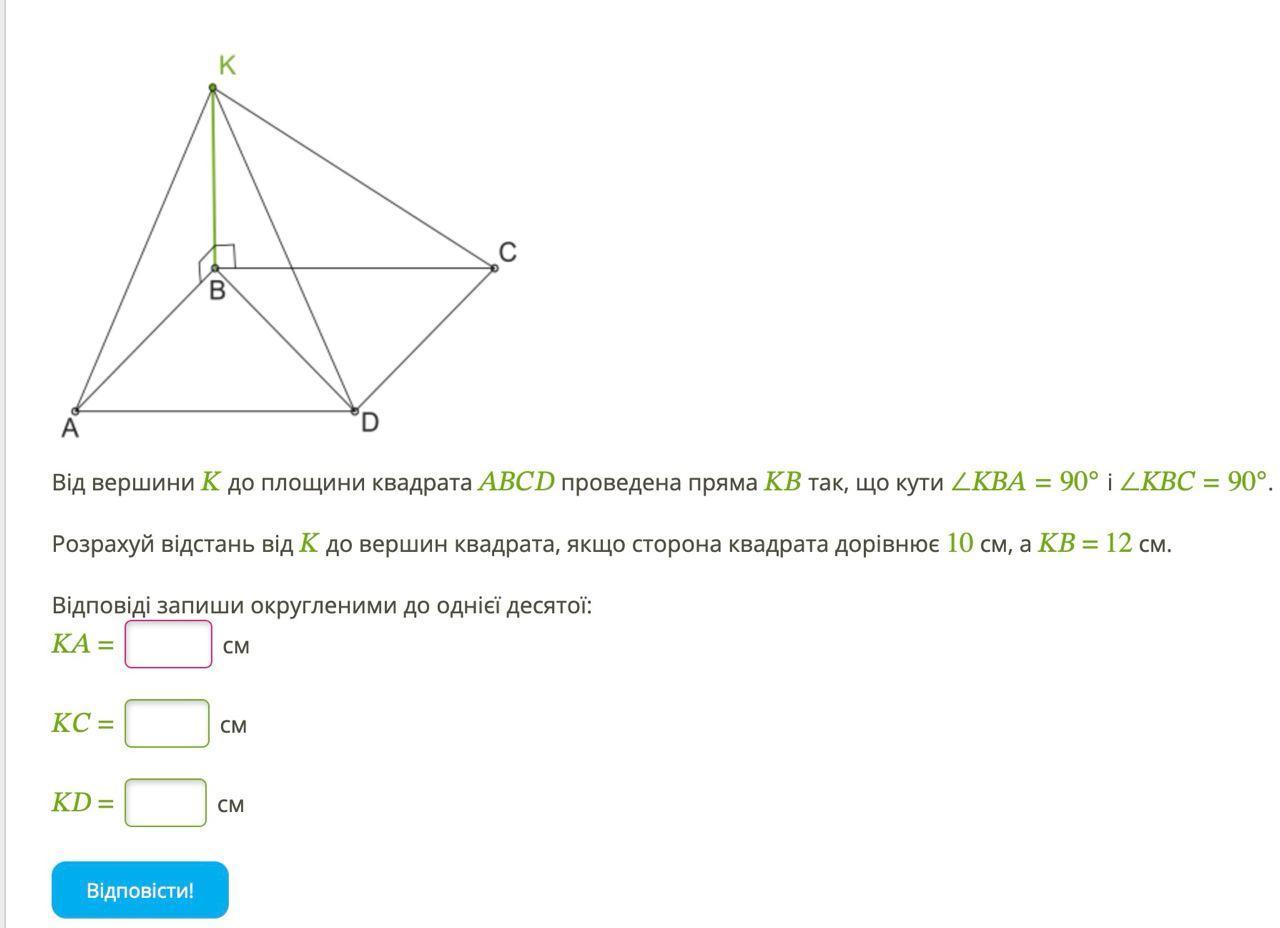
Від вершини до площини квадрата проведена пряма так, що кути ∠=90° і ∠=90°.

Розрахуй відстань від до вершин квадрата, якщо сторона квадрата дорівнює 10 см, а = 12 см.

Відповіді запиши округленими до однієї десятої:

Ответ:

Відстань від вершини до площини квадрата можна знайти за допомогою теореми Піфагора. Згідно з умовою, сторона квадрата дорівнює 10 см, тому сторона прямокутного трикутника АВС, де А - вершина квадрата, В - точка перетину прямої з площиною квадрата, С - точка на прямій, що лежить на розмітці, має довжину 12 см. Треба знайти довжину відрізку АС.

Застосуємо теорему Піфагора:

АС² = АВ² + ВС²

Замінюємо величинами:

АС² = 10² + 12²

АС² = 100 + 144

АС² = 244

Знаходимо квадратний корінь з обох боків:

АС = √244

Апроксимуємо значення:

АС ≈ 15,6 см

Таким чином, відстань від вершини до площини квадрата становить приблизно 15,6 см.