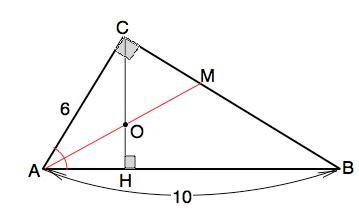
в ABC прямоугольнике, из острого A угла проведена AM биссектриса, а с прямого C угла CK высота. Найдите части, на которых биссектриса разделила высоту , если известно что AC=6 , AB=10.

пжжжж срочно ((

Ответ: 5:3 или иначе 3 и 1,8 ед. длины.

Объяснение:

  Биссектриса внутреннего угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам.=>

В ∆ АВС сторона ВС делится биссектрисой в отношении АС:АВ, т.е. 6:10=3:5

Высота прямоугольного треугольника, проведенная из вершины прямого угла, делит его на два треугольника, подобные друг другу и исходному. Следовательно, биссектриса угла А делит высоту в том же отношении, как сходственную сторону, т.е. в отношении НО:ОС=3:5.

********

Если вычислить  длину высоты, можем найти длину этих отрезков.

Обозначим высоту СН, точку пересечения АМ и СН  - буквой О.

Высота СН, проведенная из вершины прямого угла,  равна частному от деления удвоенной площади треугольника ( произведения его катетов) на гипотенузу АВ.

СН=АС•ВС:АВ=6•8:10=4,8

АО делит СН на 5+3=8 частей.

1 часть=4,8:8=0,6.=>

СО=5•0,6=3 (ед. длины).

ОН=3•0,6=1,8 (ед. длины).