Уважаемые МОЗГи! Задание, достойное Вас!!
Найти общее решение уравнения методом неизвестных коэффициентов.
Если можно, с подробным (пошаговым) решением. Заранее спасибо))
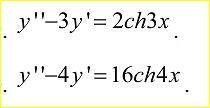
Ответы на вопрос
1) y''-3y'
Решение уравнения будем искать в виде . Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами.
Тогда систему составят функции:
Общее решение однородного уравнения: , где C ∈ R
2) 2ch3x
Ищем частное решение
R(x) и S(x) это полиномы, их степень - макс. степень полиномов P(x) и Q(x)
У нас:
Поэтому k у нас равен 1 (т.к. 0i наш корень кратности)
И уравнение имеет частное решение
y=x(Ax+B)
Находим производные, которые нужно подставить в исходное ур.
Отсюда получаем систему, приравняв коэф. при х:
Решаем и находим корни: A=0, B=
Тогда частное решение примет вид:
И теперь общее решение уравнения примет вид:
Второе решается АНАЛОГИЧНО! Пояснять решения далее не буду, все расписал в 1 примере
1)y''-3y'
2) 16ch4x
k у нас равен 1
Система;
Корни:
Вид частного решения:
И теперь общее решение уравнения примет вид: