Упростите выражения:
sin2п/15*cosп/5+cos2п/15*sinп/5
sin2п/5*cosп/15-cos2п/5*sinп/15
Ответы на вопрос
Ответил Аноним
14
Решение:
1) sin(2П/15)cos(П/5)+cos(2П/15)sin(П/5) =
sin (2pi/15 + pi/5)
sin ( 2pi/15 + 3pi/15)
sin (5pi/15)
sin (pi/3) = √3/2
2)sin 2П/5 cos П/15 - cos 2П/5 sin П/15 = sin (2П/5-cos П/15 ) =sinП/3 = √3/2
Ответ: 1)√3/2;2)√3/2
Ответил Applegate
11
Ответ:
Объяснение:
___________________
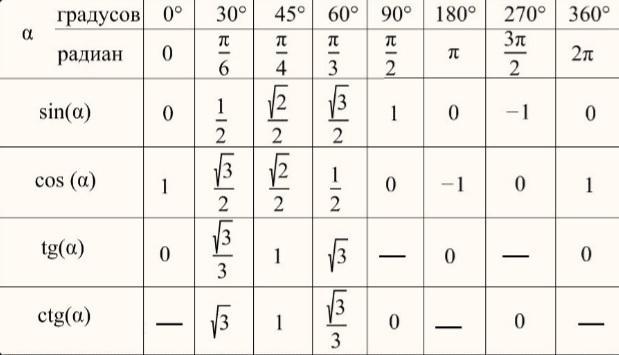
справочные материалы и формулы-на изображениях
Приложения:
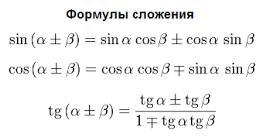
Новые вопросы