Алгебра, вопрос задал shymskay1112 , 1 год назад

Упростите выражение.
Пожалуйста помогите

Приложения:

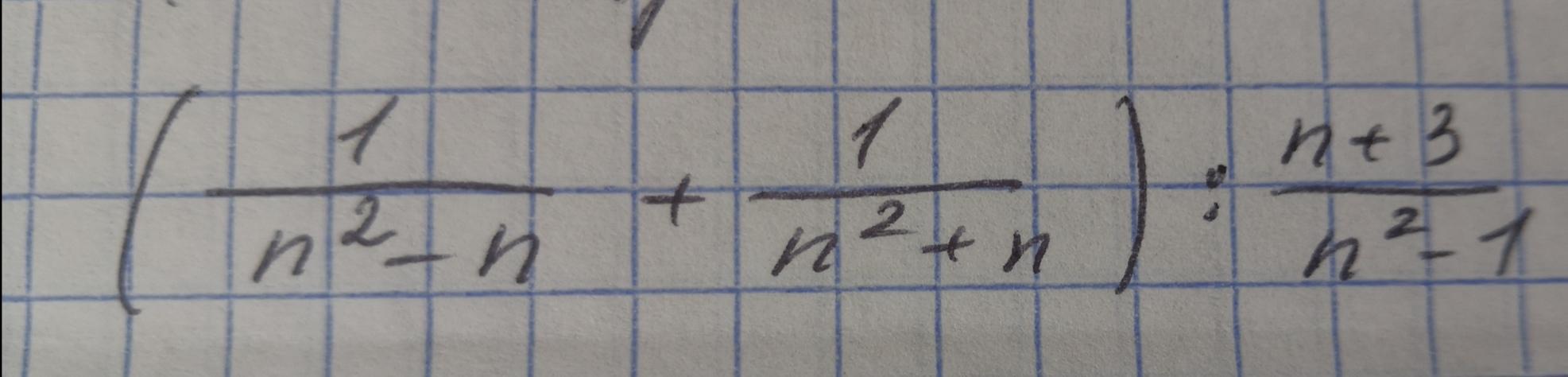
Ответы на вопрос

Ответил krikermorgard
1

(\frac{1}{n(n-1)}+\frac{1}{n(n+1)}) : \frac{n+3}{n^2-1}  =\\(\frac{n+1+n-1}{n(n+1)(n-1)} ):\frac{n+3}{n^2-1}  =\\\\\frac{2n}{n(n^2-1)} : \frac{n+3}{n^2-1}=\\\frac{2n}{n(n^2-1)}*\frac{n^2-1}{n+3} = \frac{2n}{n}*\frac{1}{n+3}  =\frac{2}{n+3}

Ответил papagenius
1

Объяснение:

\tt\displaystyle \[\left( {\frac{1}{{{n^2}-n}}+\frac{1}{{{n^2}+n}}}\right):\frac{{n+3}}{{{n^2}-1}}=\left( {\frac{{({n^2}+n)+({n^2}-n)}}{{({n^2}-n)({n^2}+n)}}} \right)*\frac{{{n^2}-1}}{{n+3}}=\frac{{2{n^2}}}{{{{\left( {{n^2}} \right)}^2}-{n^2}}}*\frac{{{n^2}-1}}{{n+3}}=\frac{{2{n^2}}}{{{n^4}-{n^2}}}*\frac{{{n^2}-1}}{{n+3}}=\frac{{2{n^2}}}{{{n^2}({n^2}-1)}}*\frac{{{n^2}-1}}{{n+3}}=\boxed{\frac{2}{{(n+3)}}}\]

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Физика, 1 год назад
Хлопцям потрібно перетягти вантаж масою 100 кг на відстань 100м. Вони починають його штовхати з постійною силою 300 Н. Коефіцієнт тертя вантажу об підлогу складає 0,25. Який час їм для цього...
Математика, 1 год назад
знайдіть площу заштрихованої частини на малюнку,допоможіть будь ласка! дам 20 балів...
Геометрия, 1 год назад
В треугольнике ABC BM-медиана и BH - высота.Известно,что AC = 112,HC = 28 угол ACB = 79.Найдите кгол AMB.18 БАЛЛОВ​...
Химия, 1 год назад
Рассчитайте относительную молекулярную массу FeCI3...
География, 6 лет назад
Английский путешественник, открывший водопад Виктория.
Математика, 6 лет назад
выполните действия 4+4 1/3 * (3- 2 5/6) : 7/36 за ранее очень благодарна (◍•ᴗ•◍)❤ ​...