Алгебра, вопрос задал ayshan , 9 лет назад

Упростите выражение!Помогите пожалуйста упростить эти четыре примера,заранее спасибо!!

Приложения:

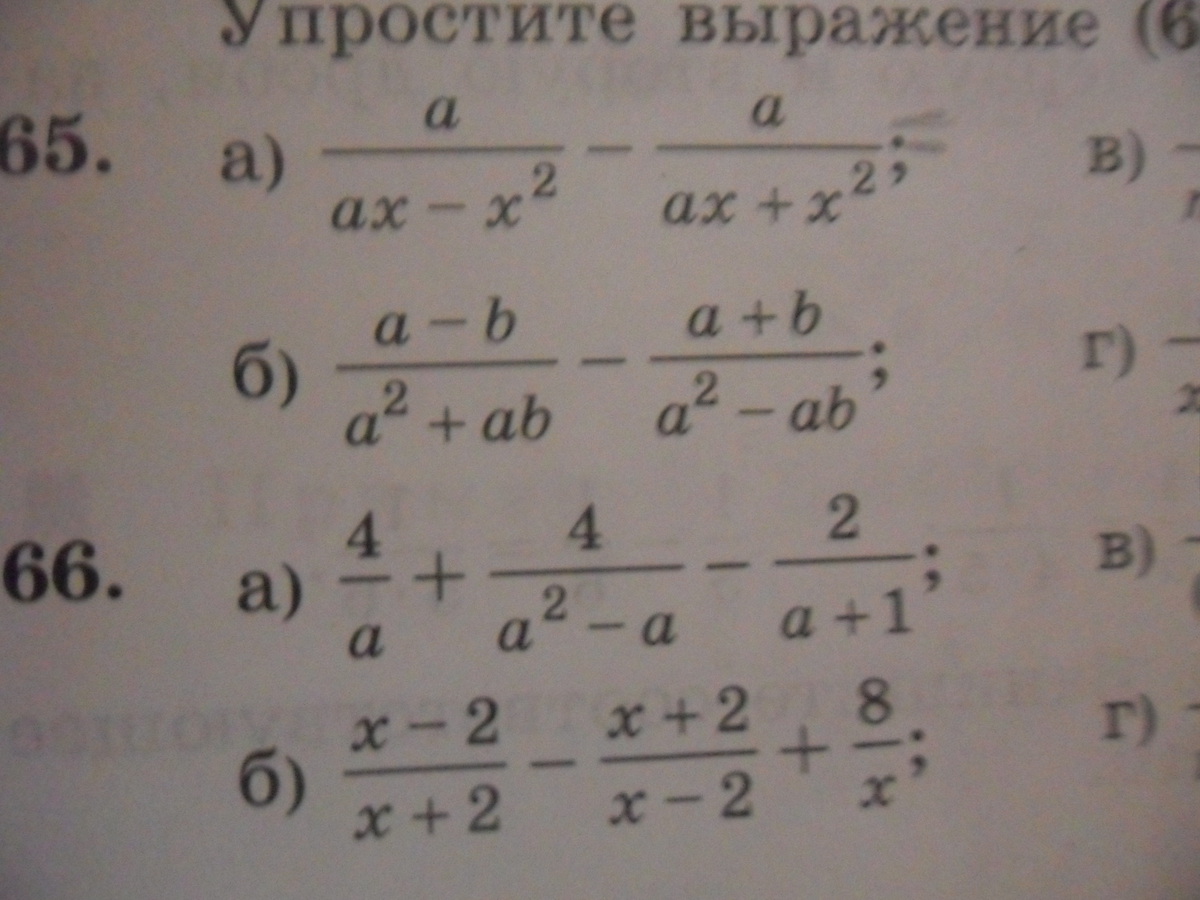
Ответы на вопрос

Ответил wangross
0
a)  frac{a}{ax- x^{2}}-frac{a}{ax+ x^{2}}=frac{a}{x(a-x)} - frac{a}{x(a+x)}=frac{ a^{2}+ax- a^{2} +ax }{x(a-x)(a+x)} = frac{2ax}{x(a-x)(a+x)}= \ = frac{2a}{(a-x)(a+x)} = frac{2a}{ a^{2}-x^{2}}

б)  frac{a-b}{a^{2}+ab} - frac{a+b}{ a^{2}-ab}=frac{a-b}{a(a+b)} - frac{a+b}{a(a-b)} = frac{(a-b)^{2}-(a+b)^{2}}{a(a+b)(a-b)} = \ =frac{a^{2}-2ab+b^{2}-a^{2}-2ab-b^{2}}{a(a+b)(a-b)}= frac{-4ab}{a(a+b)(a-b)} = frac{-4b}{(a+b)(a-b)} = frac{-4b}{a^{2}-b^{2}}

а) = frac{4}{a} + frac{4}{a(a-1)} - frac{2}{a+1} = frac{4a^{2}-4+4a+4-2a^{2}+2a}{a(a-1)(a+1)} = frac{2a^{2}+6a}{a(a-1)(a+1)} = \ = frac{2a(a+3)}{a(a-1)(a+1)}= frac{2(a+3)}{(a-1)(a+1)} = frac{2a+6}{a^{2}-1}

б)  frac{x-2}{x+2} - frac{x+2}{x-2} + frac{8}{x} = frac{(x-2)(x^{2}-2x)-(x+2)(x^{2}+2x)+8(x^{2}-4) }{x(x+2)(x-2)} = \ = frac{ x^{3}-4 x^{2} +4x- x^{3}-4x^{2}-4x+8x^{2}-32}{x(x+2)(x-2)} = frac{-8x^{2}-32}{x(x+2)(x-2)}=
= frac{-8(x^{2}+4)}{x(x+2)(x-2)}
Предыдущий вопрос
Следующий вопрос
Новые вопросы