Алгебра, вопрос задал Аноним , 2 года назад

упростите выражение.
PHOTOMATH НЕ РЕШАЕТ!!​

Приложения:

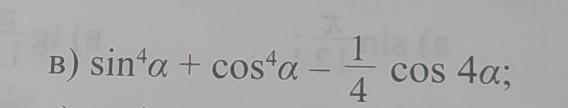
Ответы на вопрос

Ответил NNNLLL54
0

Ответ:     \dfrac{3}{4}   .

\star \ \ sin^2a+cos^2a=1\ \ \to \ \ \ (sin^2a+cos^2a)^2=1^2\ \ ,\\\\sin^4a+2\, sin^2a\cdot cos^2a+cos^4a=1\\\\sin^4a+cos^4a=1-2\, sin^2a\cdot cos^2a\\\\sin^4a+cos^4a=1-2\cdot (\underbrace{sina\cdot cosa}_{\frac{1}{2}\cdot sin2a})^2\\\\sin^4a+cos^4a=1-2\cdot \dfrac{1}{4}\, sin^22a\\\\sin^4a+cos^4a=1-\dfrac{1}{2}\, sin^22a\ \ \ \star \\\\\\sin^4a+cos^4a-\dfrac{1}{4}\, cos4a=1-\dfrac{1}{2}\, sin^22a-\dfrac{1}{4}\cdot (cos^22a-sin^22a)=

=1-\dfrac{1}{2}\, sin^22a-\dfrac{1}{4}\cdot cos^22a+\dfrac{1}{4}\, sin^22a=1-\dfrac{1}{4}\, sin^22a-\dfrac{1}{4}\cdot cos^22a=\\\\=1-\dfrac{1}{4}\cdot (\underbrace{sin^22a+cos^22a}_{1})=1-\dfrac{1}{4}=\dfrac{3}{4}

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Окружающий мир, 1 год назад
помогите пожалуйста прошу вас...
Английский язык, 1 год назад
Use the following verbs in the Past Simple. 1. I … (clean) my teeth three times yesterday. 2. It was hot in the room, so I … (open) the window. 3. When I was a child, I … (want) to be a doctor.
Другие предметы, 2 года назад
ОЧЕНЬ СРОЧНООО!!!!!!​
Математика, 2 года назад
Составь задачи по кратким записям и реши их б) . СРООООЧНООООО ПОМОГИТЕ ПЖЖЖЖ...
Математика, 8 лет назад
разность двух чисел на 16 меньше первого числа и на 4 больше второго. Найдите эти числа и разность...
Алгебра, 8 лет назад
алгебра номер 156 7...