Математика, вопрос задал Immehello , 6 лет назад

Упростить выражение
Пожалуйста​

Приложения:

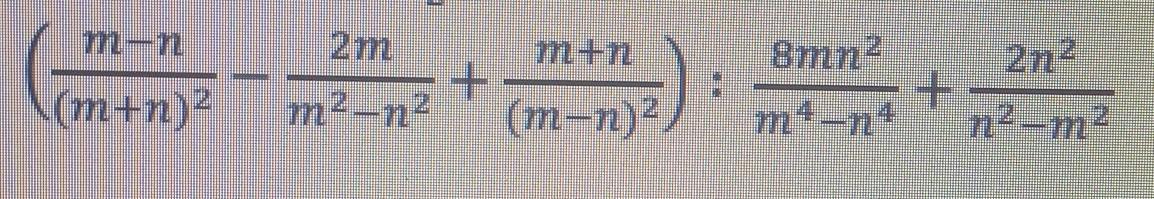
Ответы на вопрос

Ответил Universalka
1

1) \ \dfrac{m-n}{(m+n)^{2} }-\dfrac{2m}{m^{2}-n^{2}}+\dfrac{m+n}{(m-n)^{2} }=\\\\=\dfrac{(m-n)(m-n)^{2}-2m\cdot (m^{2}-n^{2})+(m+n)(m+n)^{2}}{(m-n)^{2}(m+n)^{2}} =\\\\=\dfrac{(m+n)^{3}-2m^{3}+2mn^{2}+(m+n)^{3}}{(m-n)^{2}(m+n)^{2}} =\\\\=\dfrac{m^{3}-3m^{2}n+3mn^{2} -n^{3} -2m^{3}+2mn^{2}+m^{3}+3m^{2}n+3mn^{2} +n^{3}}{(m-n)^{2}(m+n)^{2}}=\\\\=\dfrac{8mn^{2} }{(m^{2}-n^{2} )(m^{2} -n^{2})}

2) \ \dfrac{8mn^{2} }{(m^{2}-n^{2})(m^{2}-n^{2} )}:\dfrac{8mn^{2} }{m^{4}-n^{4}} =\\\\=\dfrac{8mn^{2} }{(m^{2}-n^{2})(m^{2}-n^{2} )}\cdot\dfrac{(m^{2} -n^{2})(m^{2}+n^{2}) }{8mn^{2} } =\dfrac{m^{2}+n^{2}}{m^{2}-n^{2}} \\\\\\3) \ \dfrac{m^{2}+n^{2}}{m^{2}-n^{2}} +\dfrac{2n^{2} }{n^{2}-m^{2}} =\dfrac{m^{2}+n^{2}}{m^{2}-n^{2}} -\dfrac{2n^{2} }{m^{2}-n^{2} }=\dfrac{m^{2}+n^{2}-2n^{2}}{m^{2}-n^{2} }=\\\\=\dfrac{m^{2}-n^{2}}{m^{2}-n^{2}}=\boxed1

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Математика, 1 год назад
1 марка стоит 3 р. Сколько таких можно купить за 15 рублей ? Составь и реши две задачи обратные данной задача на 2 класс...
География, 1 год назад
почему в разных водоемах разный вкус воды...
Математика, 6 лет назад
Дано вектори а (3; 4; 0) і Б (-2; 2; 6). До кожного початку речення (1-4) доберіть його закінчення (А-Д) так, щоб утворилося правильне твердження.
Алгебра, 6 лет назад
помогитепомогитепомогитепомогите​...
Математика, 8 лет назад
Помогите пожалуйста. Тригонометрия...
Математика, 8 лет назад
сократи дробь используя признаки делимости 14/21;18/24;24/15;25/35;81/108...