упростить выражение на фото:
![{( \frac{ \frac{1}{x} -x }{( \sqrt[3]{x} + \sqrt[3]{ \frac{1}{x} + 1)( \sqrt[3]{x} + \sqrt[3]{ \frac{1}{x} } - 1) } } + \sqrt[3]{x} )}^{ - 3} {( \frac{ \frac{1}{x} -x }{( \sqrt[3]{x} + \sqrt[3]{ \frac{1}{x} + 1)( \sqrt[3]{x} + \sqrt[3]{ \frac{1}{x} } - 1) } } + \sqrt[3]{x} )}^{ - 3}](https://tex.z-dn.net/?f=+%7B%28+%5Cfrac%7B+%5Cfrac%7B1%7D%7Bx%7D+-x++%7D%7B%28+%5Csqrt%5B3%5D%7Bx%7D+%2B++%5Csqrt%5B3%5D%7B+%5Cfrac%7B1%7D%7Bx%7D+%2B+1%29%28+%5Csqrt%5B3%5D%7Bx%7D+%2B++%5Csqrt%5B3%5D%7B+%5Cfrac%7B1%7D%7Bx%7D+%7D++-+1%29++%7D+++%7D+++%2B++%5Csqrt%5B3%5D%7Bx%7D+%29%7D%5E%7B+-+3%7D+)
Ответы на вопрос
Ответил NNNLLL54
0
Ответ:
Упростить выражение .
Сначала упростим выражение в скобке .
Теперь возведём полученное выражение в (-3) степень .
Окончательно получили :
Приложения:

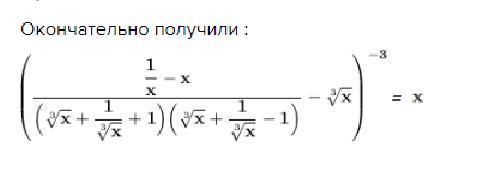
allomafayz:
на первом фото опечатка, поэтому ответ "некрасивый" вышел в строчке где сокращали (1/x -x) и (x - 1/x) забыли минус вынести
Но все равно спасибо большое!
уже поправила
Новые вопросы
Математика,
11 месяцев назад
Химия,
11 месяцев назад
Математика,
1 год назад
Русский язык,
1 год назад
Алгебра,
6 лет назад