Алгебра, вопрос задал Heisenberg228 , 8 лет назад

Умолю. Очень сложно

Приложения:

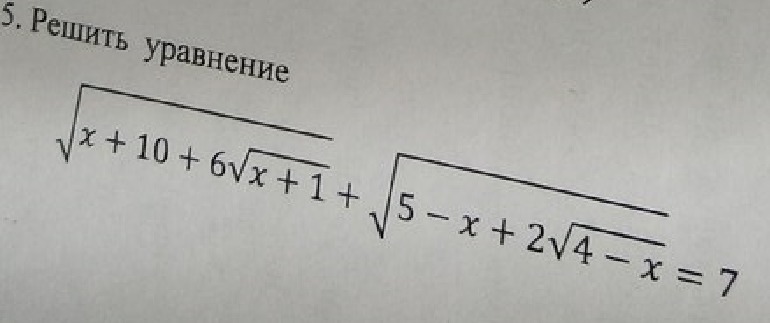
Ответы на вопрос

Ответил iLeysan

$sqrt{x+10+6 sqrt{x+1} }+ sqrt{5-x+2 sqrt{4-x} } =7$
$x+10+6 sqrt{x+1}=( sqrt{x+1}+3)^{2}$
$5-x+2 sqrt{4-x}=( sqrt{4-x}+1)^2$
$sqrt{( sqrt{x+1}+3)^2 } + sqrt{( sqrt{4-x}+1)^2 }=7$
При условии, что:
$left { {{ sqrt{x+1} geq 0 } atop { sqrt{4-x} geq 0 }} right.$
$left { {{x geq -1} atop {x leq 4}} right.$
Тогда:
$sqrt{x+1}+3+ sqrt{4-x}+1=7$
$sqrt{x+1}+ sqrt{4-x} +4=7$
$sqrt{x+1}+ sqrt{4-x}=3$
Возводим в квадрат обе части уравнения:
$( sqrt{x+1}+ sqrt{4-x})^2=9$
$x+1+4-x+2( sqrt{x+1})( sqrt{4-x})=9$
$5+2 sqrt{(x+1)(4-x)}=9$
$2 sqrt{(x+1)(4-x)}=4$
$sqrt{(x+1)(4-x)}=2$
Возведем обе части уравнения в квадрат (снова):
$(x+1)(4-x)=4$
$4x- x^{2} +4-x=4$
$- x^{2} +3x=0$
$x^{2} -3x=0$
$x(x-3)=0$
Получаем:
x=0 и x=3
Наше условие:
$left { {{ sqrt{x+1} geq 0 } atop { sqrt{4-x} geq 0 }} right.$
$left { {{x geq -1} atop {x leq 4}} right.$
- сохраняется => оба корня верны.

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Информатика, 2 года назад

Умоляю помогите с карточкой по программированию!!! Даю 65 балов...

Русский язык, 2 года назад

Задание 2 (8 баллов) Составьте из приведённых слов цепочку так, чтобы конечный звук каждого слова совпадал с начальным звуком следующего за ним слова, а конечный звук последнего слова с начальным...

Математика, 8 лет назад

Всего-31учащихся Мальчиков-17уч Девочек-?% Какую часть вашего класса составляет мальчики,в процентах.

Математика, 8 лет назад

помогите пожалуйста номер 714 ДАМ 35 БАЛЛОВ умоляю во 2 там ровно 8 целых 1 /4...

География, 9 лет назад

Что открыл фернан магеллан...

Геометрия, 9 лет назад

В каком отношении средняя линия трапеции делит её площадь, если основания трапеции равны 7см и 3см ? Пожалуйста, помогите...