УМОЛЯЮ ПОМОГИТЕ!
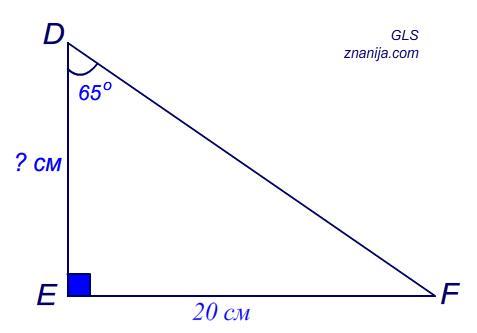
в треугольнике DЕF : угол E=90° , ЕF =20° , угол FDE=65° . Найди длину стороны DE .
Ответ округлить до 3 значащих цифр.
9,83см
9,33см
9,63см
Ответы на вопрос
Ответил ldglkva
0
Ответ:
DE ≈ 9,33 см.
Объяснение:
Дано: ΔDЕF; ∠E=90° , ЕF =20 см , ∠FDE=65°.
Найти: DE.
Решение.
В прямоугольном треугольнике котангенс острого угла равен отношению прилежащего катета к противолежащему.
В ΔDЕF:
- Значащей цифрой десятичной дроби называют ее первую (слева направо) отличную от нуля цифру, а также все следующие за ней цифры.
Котангенс угла 65° найдем из справочных таблиц Брадиса В.М. (или с помощью калькулятора) с точностью до четвертой значащей цифры, так как округлять будем до третьей значащей цифры.
Ctg 65° ≈ 0,4663;
DE = 20 см · 0,4663 = 9,326 см ≈ 9,33 см.
DE ≈ 9,33 см.
Приложения:
Новые вопросы