УМОЛЯЮ!!! ПОМОГИТЕ!!!(((

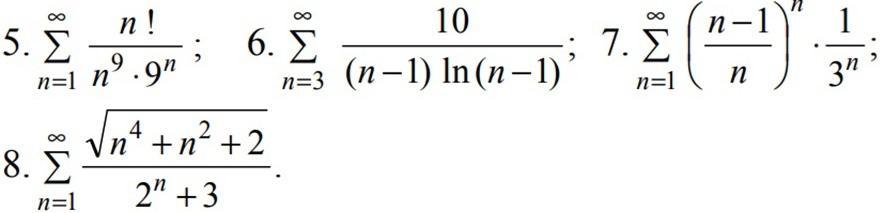
Ответы на вопрос
Ответ:
Пошаговое объяснение:
1) я бы первым делом проверила необходимое условие сходимости ряда
необходимый признак сходимости ряда. Если ряд сходится, то его n-й член стремится к нулю при n → ∞ .
этот признак не покажет сходимость, но он поможет установить расходимость ряда - если признак не выполняется, то ряд расходится.
конечно, можно сразу начать с признака Даламбера, но там на вскидку получится предел =1 и вот она - неопределенность. поэтому начнем с рассмотрения предела исходного ряда
(расписывать предел не буду, скажу только, что тут ∞/∞ и надо применить метод Лопиталя)
а у нас предел не равен 0, необходимое условие сходимости не выполняется, и, значит, , ряд расходится.
ответ ряд расходится.
2) произведем упрощение
получим ряд , применим сравнительный признак и получим, что у нас α =2 > 1 ⇒ ряд сходится
ответ ряд сходится
3) здесь уместен будет радикальный признак Коши
полученное значение меньше 1 ⇒ ряд сходится
ответ ряд сходится
4) на него уже просто не хватает сил.... может кто поможет.... извините...
там надо провести упрощения и выйти на ряд, где в числителе будет n⁻² α < 1 ряд будет расходиться по признаку сравнения....
но записывать это подробно уже устала я....