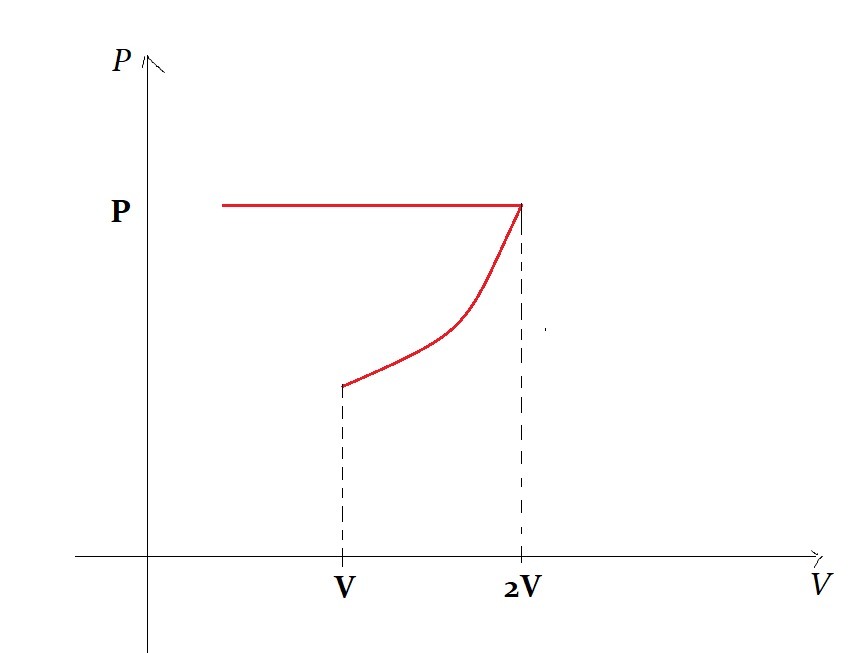
Углекислый газ, массой 400 грамм был нагрет от 350К до 420К при постоянном давлении, а затем изотермически сжат в 2 раза. Определить количество теплоты, полученное газом и совершенную им работу.

Первый закон термодинамики для изобарного (при постоянном давлении) процесса: ; В нашем случае: (1); Согласно уравнению Менделеева-Клапейрона: ; С учетом этого (1) примет вид: ;

Следующий процесс - изотермический. Он проходит при постоянной температуре, а значит внутренняя энергия газа остается неизменной.

Значит ; Работа при изотермическом сжатии считается так: ; Заметим, что газ в этом случае сжимается, т.е совершает отрицательную работу, а значит он отдает тепло. Полученное газом в итоге тепло можно считать разностью |Q| и |Q'|; Эта величина равна ;  Молярная масса M углекислого газа равна ≈0.044 кг/моль; CO₂ - трехатомная линейная молекула, поэтому число степеней свободы для нее i=5; Подставим эти данные в формулу: ; То есть газ отдал ≈42,16 Дж теплоты. Если в задаче имелось ввиду какое количество положительное количество теплоты получил газ, то ответом будет величина ;

Работа, которую совершил газ, равна