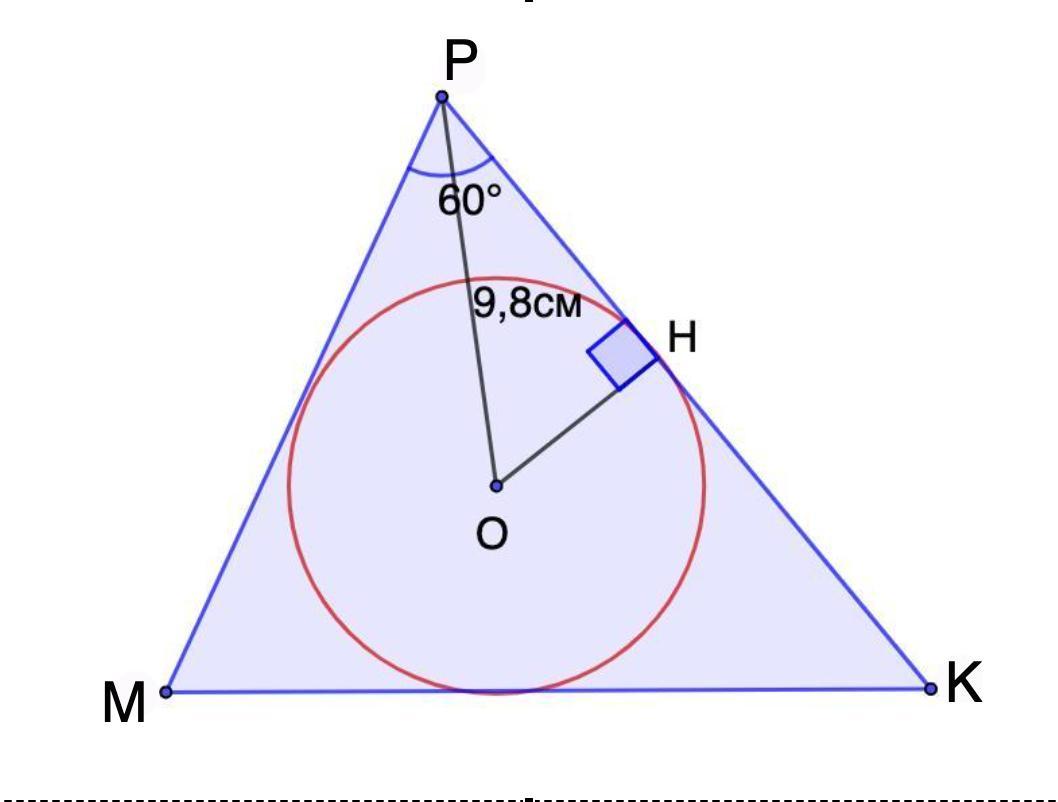
У трикутнику MPK кут P = 60*. Відстань від центра вписаного трикутник кола до вершини P дорівнює 9.8см. Знайдіть радіус цього кола...

Ответ:

Радиус вписанной окружности равен 4,9 см.

Объяснение:

В треугольнике MPK угол P = 60*. Расстояние от центра вписанного треугольник круга до вершины P равно 9.8 см. Найдите радиус этой окружности.

Дано: ΔМРК;

Окр.О - вписанная.

ОР = 9,8 см.

∠Р = 60°

Найти: R вписанной окружности.

Решение:

Рассмотрим ΔОРН.

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ОН ⊥ РК.

ΔОРН - прямоугольный.

• Центр вписанной окружности лежит на биссектрисе угла.

⇒ ∠МРО = ∠ОРК = 60° : 2 = 30°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ ОР = 2 ОН = 9,8 см

ОН = ОВ : 2 = 9,8 : 2 = 4,9 см.

Радиус вписанной окружности равен 4,9 см.