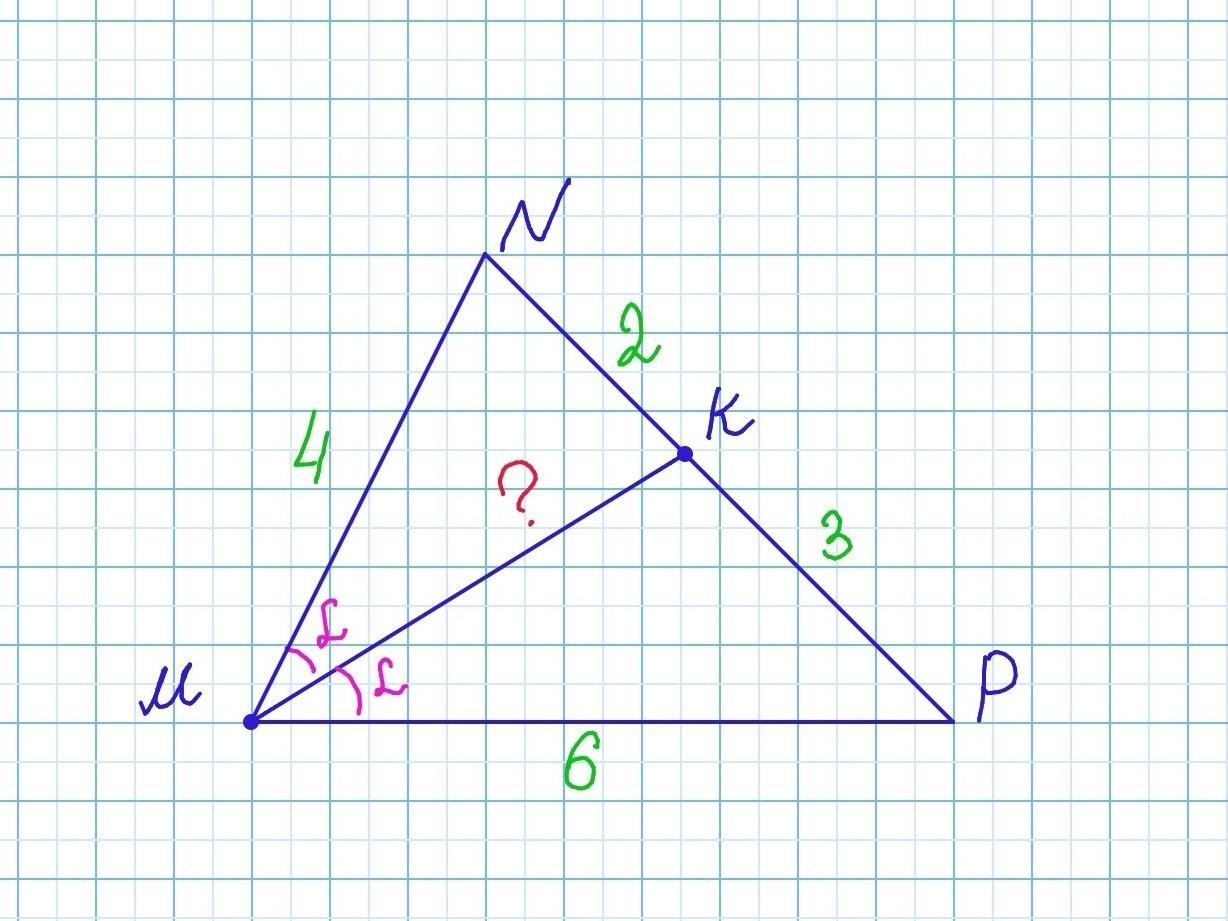
Геометрия, вопрос задал launova100707 , 6 лет назад

У трикутнику MNP MN=4, MP = 6, а на стороні NP обрано точку К так. що NK = 2, КР = 3. Знайдіть довжину MK.

Ответы на вопрос

Ответил ReMiDa

Ответ:

$3 \sqrt{2}$

ед

Объяснение:

Докажем, что МК- биссектриса. Свойство биссектрисы:

Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.

То есть должно выполняться условие:

$\dfrac{MN}{MP} = \frac{NK}{KP} \\ \\ \dfrac{4}{6} = \dfrac{2}{3} \\ \\ \dfrac{2}{3} = \dfrac{2}{3}$

равенство верное. МК - биссектриса. МК=х. ∠NMK=∠PMK= α

По теореме косинусов выразим угол α из треугольников NMK и PMK.

Треугольник NMK:

$\cos( \alpha ) = \dfrac{ {MN}^{2} + {MK}^{2} - {NK}^{2} }{2 \times MN \times MK} = \\ \\ = \dfrac{ {4}^{2} + {x}^{2} - {2}^{2} }{2 \times 4 \times x} = \dfrac{12 + {x}^{2} }{8x}$

Треугольник РMK:

$\cos( \alpha ) = \dfrac{ {MK}^{2} + {MP}^{2} - {KP}^{2} }{2 \times MK \times MP} = \\ \\ = \dfrac{ {x}^{2} + {6}^{2} - {3}^{2} }{2 \times x \times 6} = \dfrac{{x}^{2} +27}{12x}$

$\dfrac{12 + {x}^{2} }{8x} = \dfrac{ {x}^{2} + 27}{12x} \\ \\ 6 {x}^{2} + 72 = 4 {x}^{2} + 108 \\ \\ 2 {x}^{2} = 36 \\ \\ {x}^{2} = 18 \\ \\ x = 3 \sqrt{2}$

СМ=3√2 ед

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

прилагательное от слова ход...

Қазақ тiлi, 1 год назад

Нужно перевести текст.50 баллов...

Английский язык, 6 лет назад

скласти речення з (present. cont. read. play.)...

Английский язык, 6 лет назад

СРОЧНО!!! помогите пж ...

Математика, 8 лет назад

Помогите мне по геометрии,спасибо заранее,даю 20б 4)Разделите отрезок MN длиной 15 см на части пропорциональные числам 3,3,4 и номер 5 прилагается к файлу...

Математика, 8 лет назад

Два теплохода вышли на встречу один одному в 8 ч. и встретились в 13 ч. того же дня.В 8 ч. расстояние между ними было 290 км.Один теплоход плыл со скоростью 28 км/ч. С какой скоростью плыл второй...