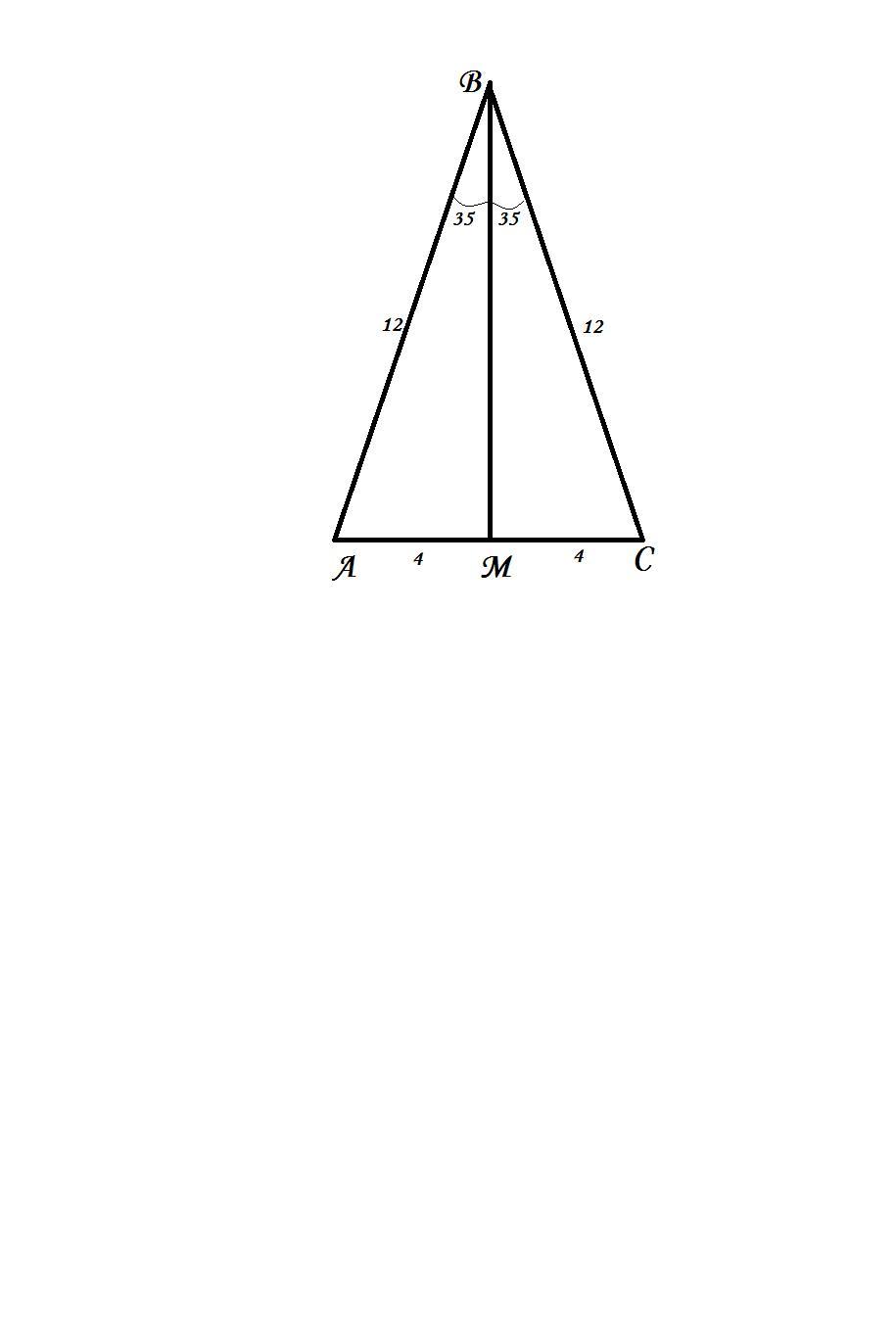
У трикутнику ABC точка M лежить на стороні AC, < AMB =<CMB , <ABM=<CBM=35⁰, AB =12 см, МC = 4 см. Знайдіть периметр трикутника АВС.
Ответы на вопрос
Ответ:
Для розв'язання даної задачі скористаємося теоремою синусів.
Спершу знайдемо значення кута AMB. Оскільки <ABM = <CBM = 35⁰, тоді <AMB = 180⁰ - <ABM - <CBM = 180⁰ - 35⁰ - 35⁰ = 110⁰.
Застосуємо теорему синусів до трикутника AMB:
AB / sin(<AMB) = MB / sin(<ABM)
12 / sin(110⁰) = MB / sin(35⁰)
MB = 12 * sin(35⁰) / sin(110⁰) = 12 * 0.5736 / 0.9397 ≈ 7.35 см.
Застосуємо теорему синусів до трикутника AMC:
AB / sin(<AMC) = MC / sin(<ACM)
12 / sin(<AMC) = 4 / sin(35⁰)
sin(<AMC) = 12 * sin(35⁰) / 4 = 12 * 0.5736 / 4 ≈ 1.72
<AMC ≈ arcsin(1.72) ≈ 61⁰.
Тепер знаходимо значення кута ACB:
<ACB = 180⁰ - <AMC - <CBM = 180⁰ - 61⁰ - 35⁰ = 84⁰.
Застосуємо теорему синусів до трикутника ABC:
AB / sin(<ACB) = BC / sin(<ABC)
12 / sin(84⁰) = BC / sin(35⁰)
BC = 12 * sin(35⁰) / sin(84⁰) = 12 * 0.5736 / 0.9080 ≈ 7.58 см.
Таким чином, периметр трикутника ABC дорівнює:
AB + BC + AC = 12 + 7.58 + 4 = 23.58 см
Ответ:
32 см.
Объяснение:
Дано: ΔАВС, т. М; ∠AMB =∠CMB , ∠ABM=∠CBM=35⁰, МС=4 см.
Р(АВС) - ?
За умовою ∠AMB =∠CMB, ∠AMB +∠CMB=180°; ∠AMB =90°; ∠CMB=90°, отже ВМ - висота.
∠ABM=∠CBM=35⁰, отже ВМ - бісектриса, а ΔАВС - рівнобедрений, АМ=СМ=4 см; АС=8 см, ВС=АВ=12 см.
Р=8+12+12=32 см.