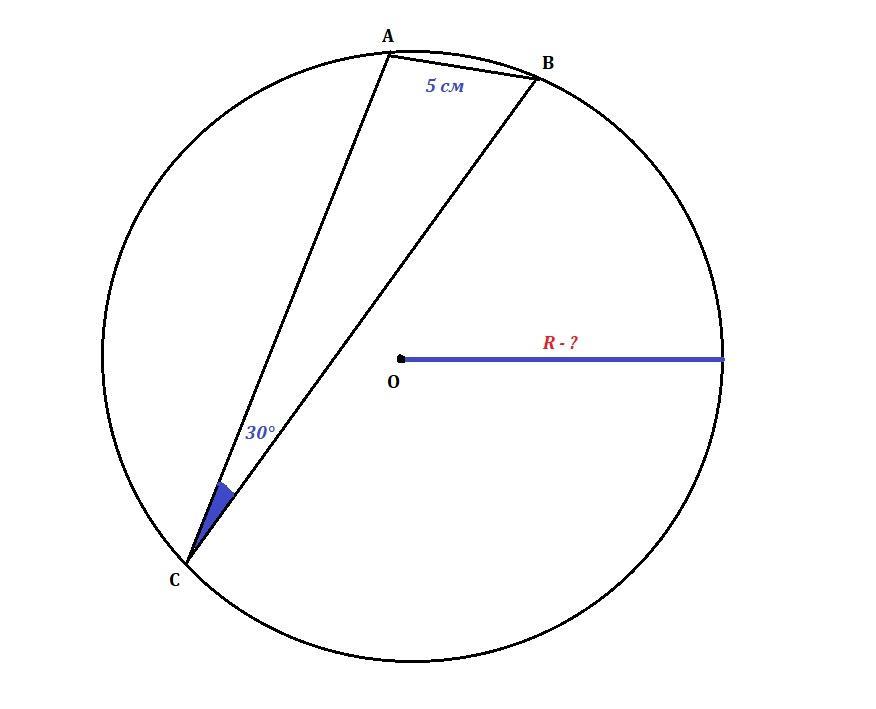
У трикутника АВС АВ = 5 см, ∠С = 30°. Знайдіть радіус кола описаного навколо трикутника.

Ответ:

5 см

Объяснение:

Теорема синусов устанавливает зависимость между сторонами треугольника и противолежащими им углами.

Для произвольного треугольника верно соотношение:

где R - радиус окружности, описанной около  треугольника

ABC.

см

Радиус окружности, описанной около треугольника равен 5 см.