У трикутник АВС вписано коло з центром у точці О, ВС=20 см. Площа трикутника ВОС дорівнює 54 см². Знайдіть радіус кола (у см).

Ответ:

Радіус кола дорівнює 5,4 см

Объяснение:

У трикутник АВС вписано коло з центром у точці О, ВС=20 см. Площа трикутника ВОС дорівнює 54 см². Знайдіть радіус кола.

Розв'язання

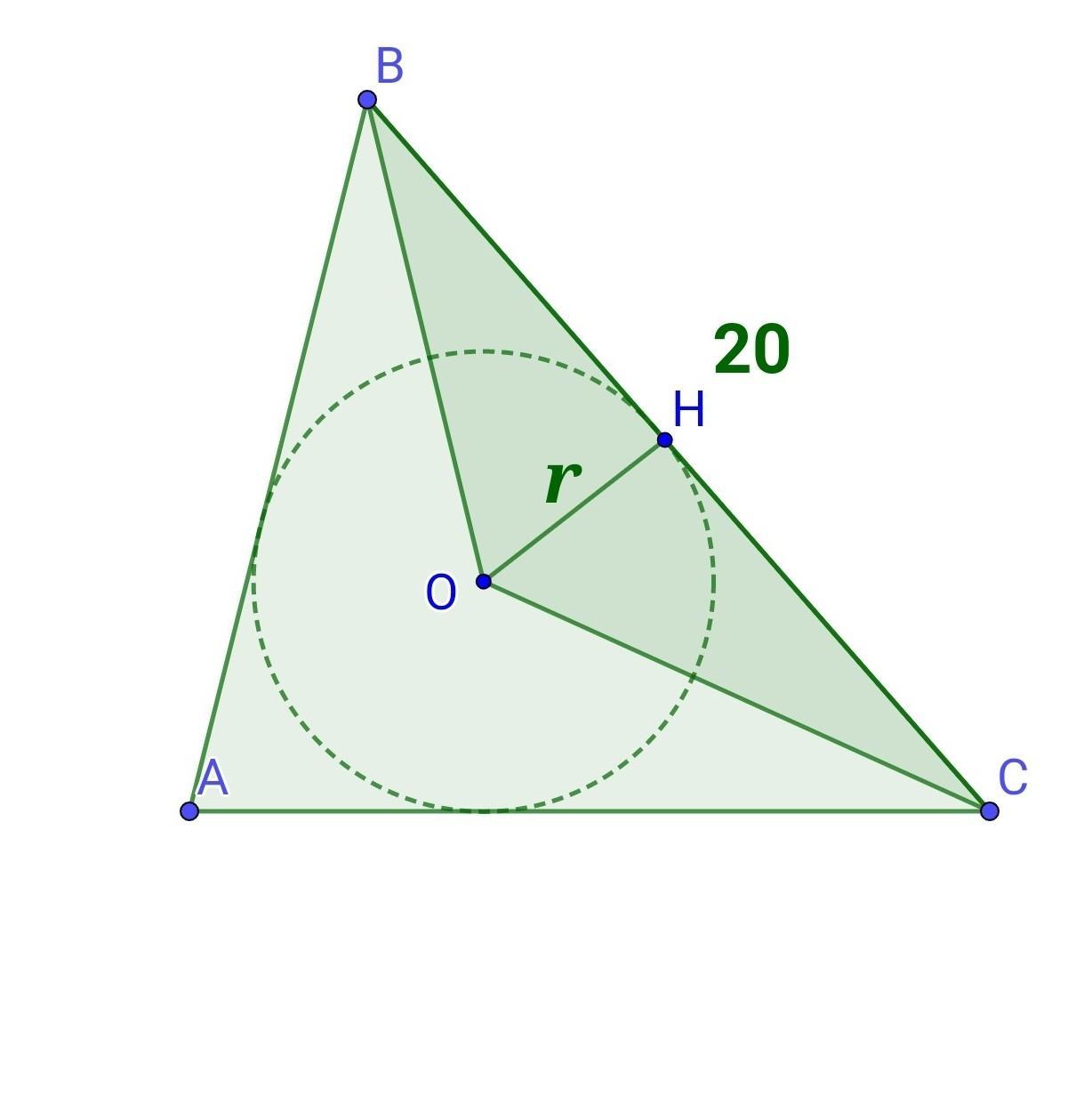
Маємо трикутник АВС, ВС = 20 см, точка О - центр вписаного кола, радіус вписаного кола - перпендикуляр, проведений з центра кола до будь-якої сторони трикутника (за властивістю дотичної до кола). ОН⟂ВС, ОН = r.

Площу трикутника знайдемо за формулою:

де а - сторона трикутника, - висота, проведена до неї.

Отже:

За умовою площа △ВОС дорівнює 54 см.

10 • r = 54

r = 5,4 (см)

Відповідь: 5,4 см

#SPJ1