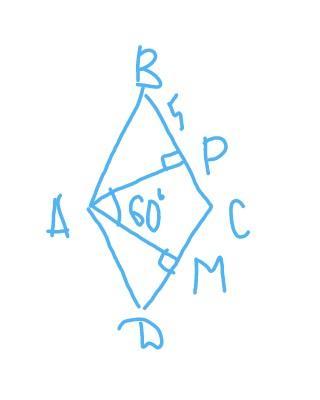
У ромбі АВСД з вершини тупого кута А проведено висоти АМ 1 АР до сторін ДС і ВС відповідно. Знайдіть периметр ромба, якщо ВР = 5

см, кут МАР дорівнює 60°.
БЕЗ СИНУСІВ,КОСИНУСІВ І Т.Д.

Объяснение:

угол между высотами ,проведенными из вершины тупого угла равен острому углу, значит ∠В=∠D=∠МАР=60°

∆АРВ - прямоугольный:

Сумма острых углов в прямоугольном тр-ке равна 90°:

∠ВАР=90-∠В=90-60=30°

Катет лежащий против угла 30° равен половине гипотенузы:

АВ=2•ВР=2•5=10 см.

Р(АВСD)=4•AB=4•10=40 см