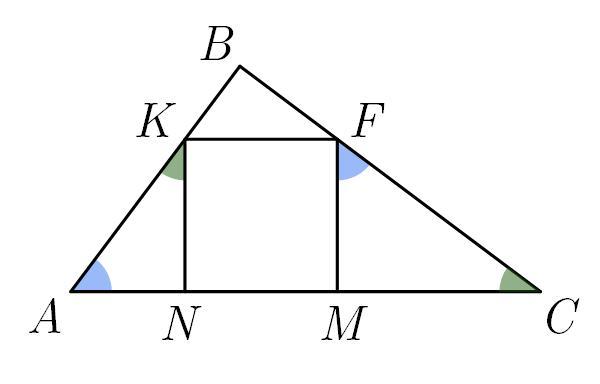
У прямокутнийтрикутник АВС ( В=900) вписано квадрат.
Знайдітьплощу квадрата, якщо АВ=12 см, ВС=16 см.
Приложения:

antonovm:
уж больно сторона квадрата некрасивая ( 240 /37 )
Перепроверил триста раз все выкладки... Таки получается так
таки 2 разных решения дают один ответ
У меня сегодня вечер плохих ответов. Будет забавно, если я таки в порыве страсти где-нибудь налажаю, приняв арифметическую ошибку за очередной плохой ответ :)
Ответы на вопрос
Ответил GoldenVoice
0
Ответ:
Площадь квадрата равна см2.
Объяснение:
Треугольники ,
и
подобны (одинаковые углы обозначены одним цветом).
Пусть сторона квадрата равна . Тогда из треугольника
Из треугольника
Значит гипотенуза
По теореме Пифагора из треугольника
Значит площадь квадрата равна
Приложения:
Ответил antonovm
0
Ответ:.........................................
Объяснение:
Приложения:
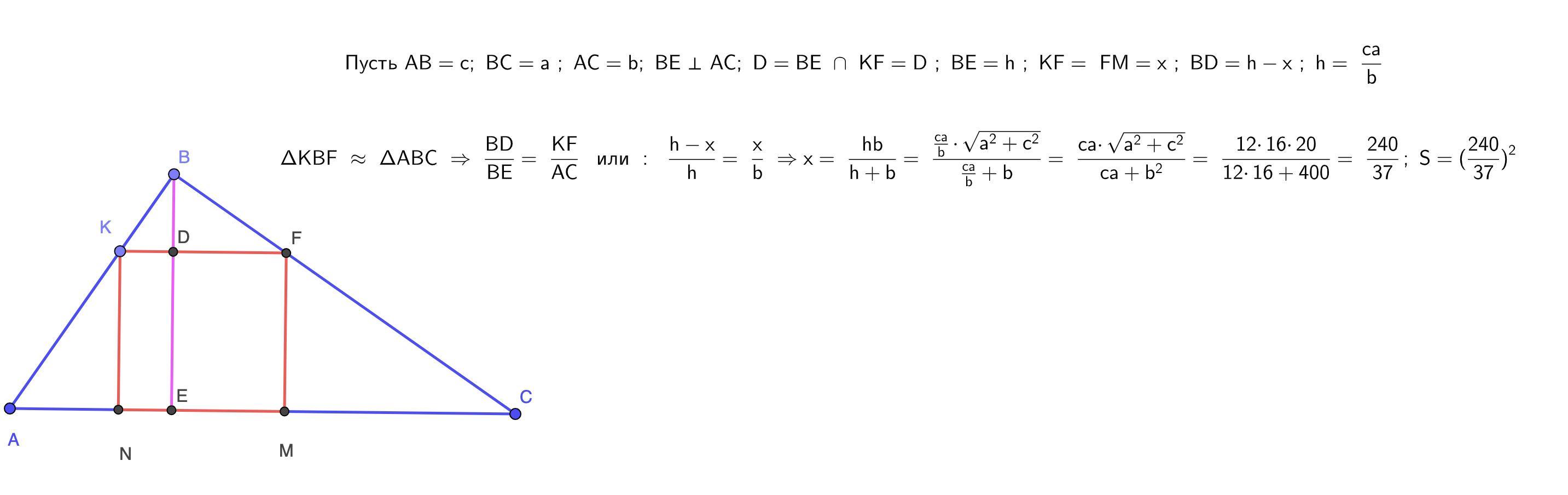
отношение сходственных высот в подобных треугольниках равно отношению сходственных сторон
Новые вопросы