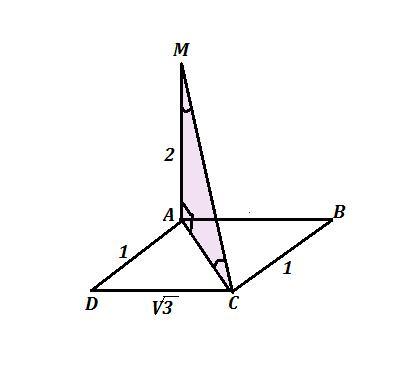
Геометрия, вопрос задал koopleasethanks , 2 года назад

У прямокутнику АВСD, відомо, що ВС=1см,
CD=корінь 3 cм. Через вершину А проведено перпендикуляр МА до площини прямокутника. Знайдіть кут між прямою МС і площиною трикутника, якщо МА=2см.
Рішення з малюнком будь ласка

mugiwaranoluffy: по теореме Пифагора: АС^2 = AD^2 +CD^2 = 1 + 3 = 4 => AC = 2
Получается что треугольник МАС - равнобедренный прямоугольный треугольник => угол МСА=45 градусов

Ответы на вопрос

Ответил NNNLLL54

Ответ:

Прямоугольник ABCD ⇒ ВС=AD=1 cм , CD=AB=√3 см .

АМ ⊥ плоскости ABCD ⇒ AM ⊥ АС , так как АМ ⊥ любой прямой, лежащей в плоскости ABCD . Значит , ΔАМС - прямоугольный и ∠МАС=90° ,

АМ=2 см .

Найдём длину АС из ΔACD , ∠ADC=90° как угол прямоугольника ABCD . По теореме Пифагора имеем

$AC^2=AD^2+CD^2\ \ ,\ \ AC^2=1^2+(\sqrt3)^2=1+3=4\ \ ,\ \ AC=\sqrt4=2$

Получили, что катеты прямоугольного ΔАМС равны по 2 см . Значит, этот треугольник равнобедренный . А так как он ещё и прямоугольный , то сумма острых углов равна 90° и ∠АМС=∠АСМ=90°:2=45° .

Угол между прямой АМ и плоскостью ABCD равен углу между наклонной АМ и её проекцией АС на эту плоскость .

Это будет угол ∠АСМ=45° .

Приложения: